题目内容
7.已知正四棱锥的侧棱与底面成60°角,则此四棱锥的底边与不相邻的侧棱所成角的余弦值是$\frac{\sqrt{2}}{4}$.分析 由题意画出图形,设正四棱锥的底面边长为a,可得AC=$\sqrt{2}a$,AO=$\frac{\sqrt{2}}{2}a$,再由侧棱与底面成60°角,求得侧棱长,解直角三角形可得四棱锥的底边与不相邻的侧棱所成角的余弦值.
解答 解:如图,设正四棱锥的底面边长为a,则AC=$\sqrt{2}a$,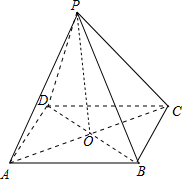
∴AO=$\frac{\sqrt{2}}{2}a$,又侧棱与底面成60°角,∴PA=$\sqrt{2}a$,PB=$\sqrt{2}a$,
在△PAB中,由$PA=PB=\sqrt{2}a$,AB=a,
可得cos∠PAB=$\frac{\frac{a}{2}}{\sqrt{2}a}=\frac{\sqrt{2}}{4}$.
∴四棱锥的底边与不相邻的侧棱所成角的余弦值是$\frac{\sqrt{2}}{4}$.
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题考查异面直线所成角,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
17.已知反比例函数y=$\frac{6}{x}$的图象与正比例函数y=$\frac{2}{3}$x的图象交于A,B两点,B点坐标为(-3,-2),则A点的坐标为( )
| A. | (-1,-6) | B. | (1,6) | C. | (3,2) | D. | (2,3) |
18.在△ABC中,A=$\frac{π}{6},BC=\frac{{4\sqrt{3}}}{3}$,AB=4,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{2}$ |