题目内容
已知椭圆G:.过点(m,0),作圆 的切线
的切线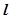 ,交椭圆G于A,B两点.
,交椭圆G于A,B两点.
(I)求椭圆G的焦点坐标和离心率; (II)将 表示为m的函数,并求
表示为m的函数,并求 的最大值.
的最大值.
【答案】
解:(Ⅰ)解:(Ⅰ)由已知得 所以
所以
所以椭圆G的焦点坐标为 离心率为
离心率为 …………2分
…………2分
(Ⅱ)由题意知, .
.
当 时,切线l的方程
时,切线l的方程 ,点A、B的坐标分别为
,点A、B的坐标分别为
此时 当m=-1时,同理可得
当m=-1时,同理可得 ………4分
………4分
当 时,设切线l的方程为
时,设切线l的方程为
由
设A、B两点的坐标分别为 ,则
,则
 ………………6分
………………6分
又由 与圆
与圆  相切得
相切得 ,即
,即
所以


所以 .
.

由于当 时,
时,
且当 时,|AB|=2,所以|AB|的最大值为2.
时,|AB|=2,所以|AB|的最大值为2.
【解析】略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 已知椭圆G:
已知椭圆G: 如图,已知椭圆G:
如图,已知椭圆G: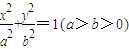 过点A(0,5),B(-8,3),直线CD过坐标原点O,且在线段AB的右下侧,求:
过点A(0,5),B(-8,3),直线CD过坐标原点O,且在线段AB的右下侧,求: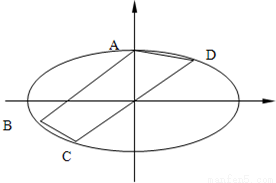
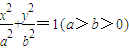 过点A(0,5),B(-8,3),直线CD过坐标原点O,且在线段AB的右下侧,求:
过点A(0,5),B(-8,3),直线CD过坐标原点O,且在线段AB的右下侧,求: