题目内容
已知过抛物线x2=
y的焦点且倾斜角为
的直线与圆x2+y2=4相交于A、B两点，P是优弧AB上任意一点，则∠APB等于 ．
| 6 |
| 3π |
| 4 |
考点：抛物线的简单性质
专题：直线与圆
分析：先求圆心到直线的距离，从而求出AB所对的圆心角，进而求出∠APB．
解答：
解：过抛物线x2=
y的焦点且倾斜角为
的直线的方程为：x+y-
=0，
∴：圆心到直线的距离d=
=
，
∠AOB═2arccos
，
∴∠APB=arccos
．
| 6 |
| 3π |
| 4 |
| ||
| 4 |
∴：圆心到直线的距离d=
| ||||
|
| ||
| 2 |
∠AOB═2arccos
| ||
| 8 |
∴∠APB=arccos
| ||
| 8 |
点评：本题主要考查直线与圆相交问题，利用圆心到直线的距离求解时关键．
练习册系列答案
相关题目
在△ABC中，内角A、B、C的对边分别a、b、c，若
=
，sinC=2
sinB，则tana=（ ）
| a |
| b |
b+
| ||
| a |
| 3 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、-
|
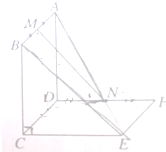如图，已知两个正方形ABCD和DCEF不在同一平面内，M，N分别为AB，DF的中点．
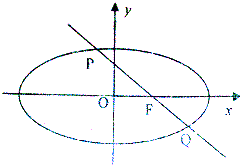已知椭圆的中心在原点，右焦点为F（3，0）过焦点F的直线l交P，Q两点线段PQ的中点为M（2，1）．求：