题目内容
19．（x-$\frac{1}{\sqrt{x}}$）6的展开式中x3的系数为15，（用数字作答）分析 在二项展开式的通项公式中，令x的幂指数等于3，求出r的值，即可求得展开式中含x3的项的系数．
解答 解：（x-$\frac{1}{\sqrt{x}}$）6的展开式的通项公式为 Tr+1=C6r•（-1）r•${x}^{6-\frac{3}{2}r}$，令6-$\frac{3}{2}$r=3，可得r=2，
故展开式中含x3的项的系数为C62=15，
故答案为：15．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
9．已知随机变量ξ的分布列为：
若$P（{ξ^2}＜x）=\frac{11}{12}$，则实数x的取值范围是（ ）
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{12}$ | $\frac{4}{12}$ | $\frac{1}{12}$ | $\frac{2}{12}$ | $\frac{1}{12}$ |
| A． | 4＜x≤9 | B． | 4≤x＜9 | C． | x＜4或x≥9 | D． | x≤4或x＞9 |
7．若a=30.3，b=logπ3，c=log0.3e，则（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | b＞c＞a |
14．阅读程序框图，运行相应的程序，则输出s的值为（ ）
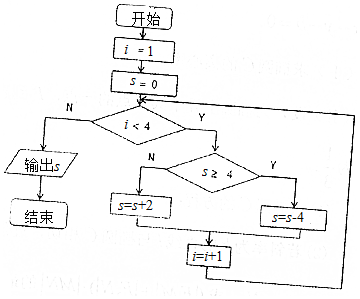
| A． | 0 | B． | 2 | C． | 4 | D． | 6 |
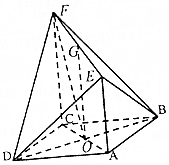如图，四边形ABCD为菱形，∠ABC=60°，AC与BD相交于点O，AE⊥平面ABCD，CF⊥平面ABCD，AB=AE=2，G为EF中点．