题目内容
14.已知函数f(x)是定义在R上的奇函数,f(x)在[0,+∞)上是增函数,若f(2m-1)+f(m2+1)>0,则m的取值范围为m<-2或m>0.分析 利用函数的奇偶性、单调性可去掉不等式中的符号“f”,转化为具体不等式,解出即可.
解答 解:∵f(x)是R上的奇函数,
∴f(2m-1)+f(m2+1)>0,可化为f(m2+1)>f(1-2m)
又f(x)在[0,+∞)上是增函数,
∴f(x)在R上是增函数,
∴m2+1>1-2m,解得m<-2或m>0,
故答案为:m<-2或m>0.
点评 本题考查函数的奇偶性单调性的综合应用,属基础题,解决本题的关键是利用函数的性质化抽象不等式为具体不等式.

练习册系列答案
相关题目
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P是直线x=a上一点,且PF1⊥PF2,|PF1|+|PF2|=2$\sqrt{2}$a,则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\sqrt{3}$ |

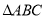 中,
中,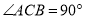 ,
,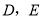 分别为
分别为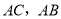 的中点,
的中点,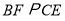 交
交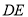 的延长线于点
的延长线于点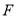 .
.
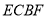 是平行四边形;
是平行四边形; 时,求证:四边形
时,求证:四边形