题目内容
已知函数f(x)＝x－1＋
x2－2，试利用基本初等函数的图象，判断f(x)有几个零点，并利用零点存在性定理确定各零点所在的区间．(各区间长度不超过1)
解析： 由f(x)＝0，得x－1＝－x2＋2.
令y1＝x－1，y2＝－x2＋2，在同一直角坐标系中分别画出它们的图象(如图所示)，其中抛物线的顶点坐标为(0,2)，与x轴的交点分别为(－2,0)，(2,0)，y1与y2的图象有3个交点，由此可知函数f(x)有3个零点．
∵f(－3)＞0，f(－2)＜0，f(1)＜0，f(2)＞0，
∴f(x)的零点所在的区间为(－3,2)，(0,1)，(1,2)．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
且
，函数
若数列
满足
，且
}(n∈N*)的前n项和为( )
(B)
(C)
(D)
D.
lg 2
的定义域为________．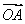
＝(1，－3)，
＝(2，－1)，
＝(k＋1，k－2)，若A，B，C三点能构成三角形，则实数k应满足的条件是________．
＝
，P是BN上的一点，若
＝m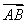
＋
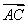，则实数m的值为( )
B.