题目内容
已知方向向量为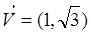
的直线l过椭圆
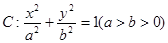的焦点以及点（0，
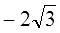），直线l与椭圆C交于 A 、B 两点，且A、B两点与另一焦点围成的三角形周长为
。
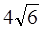（1）求椭圆C的方程
（2）过左焦点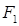
且不与x轴垂直的直线m交椭圆于M、N两点，
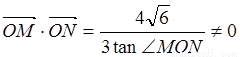（O坐标原点），求直线m的方程
【答案】
（1）
（2）
【解析】本试题主要是考查了椭圆方程的求解和直线与椭圆位置关系的运用。利用椭圆的几何性质，来表示得到a,b,c的值，从而解得方程，然后设出直线方程，联立方程组，借助于韦达定理，运用代数的方法来表示坐标，同时借助于题目中向量的关系式，得到坐标的关系，消去坐标，得参数的关系式，进而求解得到。解：（1）
直线
与x轴交点即为椭圆的右焦点
∴c=2
由已知⊿
周长为
，则4a=，即
，所以
故椭圆方程为
（2）椭圆的左焦点为
，则直线m的方程可设为
代入椭圆方程得：
设
∵
所以，
，即
又
原点O到m的距离
，则
解得
练习册系列答案
名校课堂系列答案
相关题目
的直线l过点（0，－2
）和椭圆C：
的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
，
的直线l过点（
）和椭圆
的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
=
，cot∠MON≠0（O为原点）.若存在，求直线m的方程；若不存在，请说明理由.
的直线
过椭圆C：＝1(a＞b＞0)的焦点以及点(0，
)，椭圆C的中心关于直线
交椭圆C于点M、N，且满足
，(O为坐标原点)，求直线
的直线l过椭圆
的焦点以及点（0，
），直线l与椭圆C交于 A 、B两点，且A、B两点与另一焦点围成的三角形周长为
。
且不与x轴垂直的直线m交椭圆于M、N两点，
（O坐标原点），求直线m的方程
的直线
点
和椭圆
的焦点，且椭圆C的中心关于直线
的直线
交椭圆C于点M，N且满足
（O为原点），若存在求出直线