题目内容
已知方向向量为![]() 的直线
的直线![]() 过椭圆C:=1(a>b>0)的焦点以及点(0,
过椭圆C:=1(a>b>0)的焦点以及点(0,![]() ),椭圆C的中心关于直线
),椭圆C的中心关于直线![]() 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
⑵过点E(-2,0)的直线![]() 交椭圆C于点M、N,且满足
交椭圆C于点M、N,且满足![]() ,(O为坐标原点),求直线
,(O为坐标原点),求直线![]() 的方程。
的方程。
(1)椭圆C的方程为![]()
(2)直线![]() 的方程为
的方程为 ![]()
解析:
⑴直线![]() ①,过原点垂直于
①,过原点垂直于![]() 的直线方程为
的直线方程为![]() ②
②
解①②得![]() ,∵椭圆中心O(0,0)关于直线
,∵椭圆中心O(0,0)关于直线![]() 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
∴![]() , …………………(2分)
, …………………(2分)
∵直线![]() 过椭圆焦点,∴该焦点坐标为(2,0),∴
过椭圆焦点,∴该焦点坐标为(2,0),∴![]() ,
,
故椭圆C的方程为![]() ③…………………(4分)
③…………………(4分)
⑵当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,代入③并整理得
,代入③并整理得
![]() ,设
,设![]() ,
,
则![]() ……………(5分)
……………(5分)
∴![]() ,……(7分)
,……(7分)
点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
∵![]() ,即
,即![]() ,
,
又由![]() 得
得 ![]() ,
,
∴![]() ,…………………………(9分)
,…………………………(9分)
而![]() ,∴
,∴![]() ,即
,即![]() ,
,
解得![]() ,此时
,此时![]() …………………………………(11分)
…………………………………(11分)
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,也有
,也有![]() ,
,
经检验,上述直线![]() 均满足
均满足![]() ,
,
故直线![]() 的方程为
的方程为 ![]()

练习册系列答案
相关题目
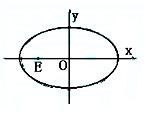

 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0, ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为 。
。 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程