题目内容
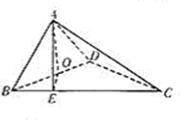
(本小题满分13分)如图,四面体ABCD中,O是BD的中点,
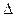 ABD和
ABD和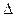 BCD均为等边三角形,AB=2,
BCD均为等边三角形,AB=2, AC=
AC=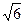 。
。
(1)求证:AO⊥平面BCD; (2)求二面角A—BC—D的大小;
(2)求二面角A—BC—D的大小;
(3)求O点到平面ACD的距离。
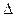 ABD和
ABD和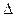 BCD均为等边三角形,AB=2,
BCD均为等边三角形,AB=2, AC=
AC=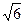 。
。
(1)求证:AO⊥平面BCD;
 (2)求二面角A—BC—D的大小;
(2)求二面角A—BC—D的大小;(3)求O点到平面ACD的距离。
(Ⅰ)证明见解析。 (Ⅱ) arctan2(Ⅲ)
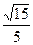
法一:(1)证明:连结OC,∵
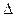 ABD为等边三角形,O为BD的中点,∴AO垂直BD。(1分)∴ AO=CO=
ABD为等边三角形,O为BD的中点,∴AO垂直BD。(1分)∴ AO=CO=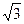 。……(2分)在
。……(2分)在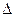 AOC中,AC=
AOC中,AC=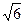 ,∴AO2+CO2=AC2,
,∴AO2+CO2=AC2,∴∠AOC=900,即AO⊥OC。∴BD
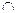 OC=O,∴AO⊥平面BCD。……(3分)
OC=O,∴AO⊥平面BCD。……(3分)(2)过O作OE垂直BC于E,连结AE,∵AO⊥平面BCD,∴AE在平面BCD上的射影为OE。
∴AE⊥BC。∠AEO为二面角A—BC—D的平面角。……(7分)
在Rt
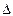 AEO中,AO=
AEO中,AO=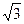 ,OE=
,OE=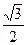 ,
,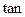 ∠
∠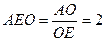 ,∴∠AEO=arctan2。
,∴∠AEO=arctan2。二面角A—BC—D的大小为arctan2。
(3)设点O到面ACD的距离为
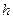 ∵VO-ACD=VA-OCD,∴
∵VO-ACD=VA-OCD,∴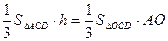 。
。在
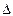 ACD中,AD=CD=2,AC=
ACD中,AD=CD=2,AC=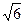 ,
,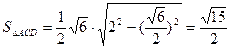 。
。
|
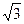 ,
,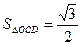 ,∴
,∴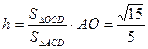 。 ∴点O到平面ACD的距离为
。 ∴点O到平面ACD的距离为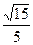 。…(13分)
。…(13分)解法二:(1)同解法一。
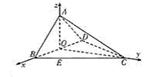
(2)以O为原点,如图建立空间直角坐标系,
则O(0,0,0),A(0,0,
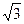 ),B(1,0,0),C(0,
),B(1,0,0),C(0,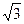 ,0),D(-1,0,0)
,0),D(-1,0,0)∵AO⊥平面DCD, ∴平面BCD的法向量
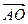 =(0,0,
=(0,0,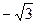 )。…(5分)
)。…(5分)
|
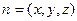 ,
, 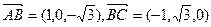 ,
,由
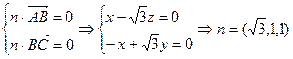 。设
。设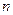 与
与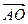 夹角为
夹角为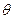 ,
,则
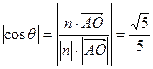 。∴二面角A—BC—D的大小为arccos
。∴二面角A—BC—D的大小为arccos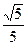 。………(8分)
。………(8分)(3)解:设平面ACD的法向量为
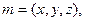 又
又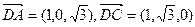
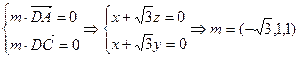 。……(11分)
。……(11分)设
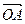 与
与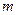 夹角为
夹角为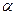 ,则
,则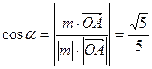 设O到平面ACD的距离为
设O到平面ACD的距离为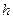 ,
,∵
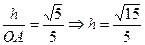 ,∴O到平面ACD的距离为
,∴O到平面ACD的距离为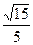 。(13分)
。(13分)
练习册系列答案
相关题目
 中,面
中,面 为矩形,
为矩形,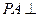 面
面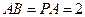
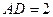 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;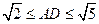 时,求二面角
时,求二面角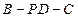 的取值范围。
的取值范围。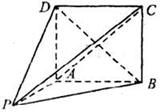
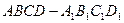 中,点
中,点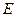 在棱
在棱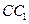 的延长线上,
的延长线上,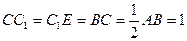 .
.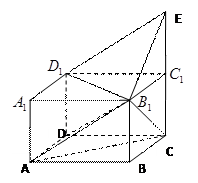
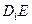 //平面
//平面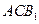 ;
; (Ⅱ) 求证:平面
(Ⅱ) 求证:平面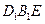
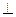 平面
平面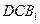 ;
;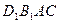 的体积.
的体积.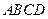 中,
中,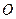 是
是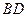 的中点,
的中点,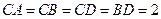 ,
,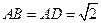 .(Ⅰ)求证:
.(Ⅰ)求证: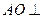 平面
平面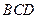 ;(Ⅱ)求异面直线
;(Ⅱ)求异面直线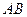 与
与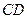 所成角的大小;
所成角的大小;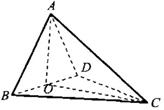
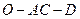 的大小.
的大小.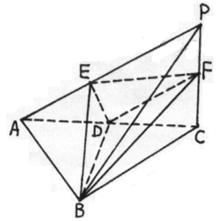
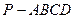 的底面为正方形,
的底面为正方形,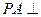 底面
底面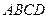 ,
,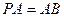 ,
,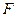 为
为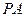 上的点.
上的点.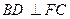 ;
;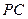 //平面
//平面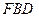 ,求二面角
,求二面角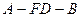 的余弦值.
的余弦值.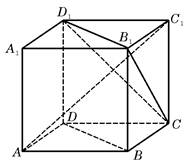
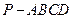 中,
中,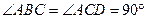 ,
,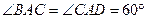 ,
,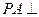 底面
底面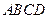 ,
,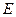 为
为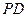 的中点,
的中点,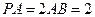 .
.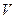 ;
;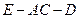 的大小.
的大小.
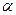 ⊥平面
⊥平面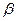 ,那么
,那么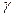 ,平面
,平面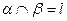 ,那么
,那么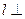 平面
平面