题目内容
已知直线l经过直线3x+4y﹣2=0与直线2x+y+2=0的交点P,且垂直于直线x﹣2y﹣1=0.求:
(Ⅰ)直线l的方程;
(Ⅱ)直线l与两坐标轴围成的三角形的面积S.
解:(Ⅰ)由 解得
解得 由于点P的坐标是(﹣2,2).
由于点P的坐标是(﹣2,2).
则所求直线l与x﹣2y﹣1=0垂直,可设直线l的方程为2x+y+m=0.
把点P的坐标代入得2×(﹣2)+2+m=0,即m=2.
所求直线l的方程为2x+y+2=0.
(Ⅱ)由直线l的方程知它在x轴.y轴上的截距分别是﹣1.﹣2,
所以直线l与两坐标轴围成三角形的面积 .
.

练习册系列答案
相关题目
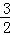 )∪(
)∪(
 B的子集个数为( )
B的子集个数为( ) )
)  的值域是( )
的值域是( ) 的定义域是( )
的定义域是( )