题目内容
7.已知三棱锥P-ABC的四个顶点都在球O的球面上,△ABC是边长为2$\sqrt{3}$的正三角形,PA⊥平面ABC,若三棱锥P-ABC的体积为2$\sqrt{3}$,则球O的表面积为20π.分析 由三棱锥P-ABC的体积为2$\sqrt{3}$,求出PA,将三棱锥补成三棱柱,可得球心在三棱柱的中心,球心到底面的距离d等于三棱柱的高PA的一半,求出球的半径,然后求出球的表面积.
解答 解:∵三棱锥P-ABC的体积为2$\sqrt{3}$,
∴$\frac{1}{3}$×$\frac{\sqrt{3}}{4}×(2\sqrt{3})^{2}PA$=2$\sqrt{3}$,
∴PA=2,
将三棱锥补成三棱柱,可得球心在三棱柱的中心,
球心到底面的距离d等于三棱柱的高PA的一半,
∵△ABC是边长为2$\sqrt{3}$的正三角形,
∴△ABC外接圆的半径r=2,
∴球的半径为$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴球O的表面积为4π×5=20π.
故答案为:20π
点评 本题考查球的内接体与球的关系,考查空间想象能力,利用割补法结合球内接多面体的几何特征求出球的半径是解题的关键.

练习册系列答案
相关题目
17.用反证法证明“平面四边形中至少有一个内角不超过90°”,下列假设中正确的是 ( )
| A. | 假设有两个内角超过90° | B. | 假设有三个内角超过90° | ||
| C. | 假设至多有两个内角超过90° | D. | 假设四个内角均超过90° |
19.下列说法正确的是( )
| A. | 过空间三点有且只有一个平面 | |
| B. | 若两个平面都和第三个平面垂直,则这两个平面平行 | |
| C. | 若两条直线都和第三条直线垂直,则这两条直线平行 | |
| D. | 垂直于同一平面的两条直线平行 |
12.某企业生产的一种产品的广告费用x(单位:万元)与销售额y(单位:万元)的统计数据如表:
(1)根据上述数据,求出销售额y(万元)关于广告费用x(万元)的线性回归方程;
(2)如果企业要求该产品的销售额不少于36万元,则投入的广告费用应不少于多少万元?
(参考数值:$\sum_{i=1}^{5}{x}_{i}=15$,$\sum_{i=1}^{5}{y}_{i}=150$,$\sum_{i=1}^{5}{x}_{i}{y}_{i}=570$,$\sum_{i=1}^{5}{{x}_{i}}^{2}=55$,$\sum_{i=1}^{5}{{y}_{i}}^{2}=6000$.
回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
| 广告费用x | 1 | 2 | 3 | 4 | 5 |
| 销售额y | 10 | 15 | 25 | 45 | 55 |
(2)如果企业要求该产品的销售额不少于36万元,则投入的广告费用应不少于多少万元?
(参考数值:$\sum_{i=1}^{5}{x}_{i}=15$,$\sum_{i=1}^{5}{y}_{i}=150$,$\sum_{i=1}^{5}{x}_{i}{y}_{i}=570$,$\sum_{i=1}^{5}{{x}_{i}}^{2}=55$,$\sum_{i=1}^{5}{{y}_{i}}^{2}=6000$.
回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
 在三棱锥P-ABC中,PA、PB、PC两两垂直,AC=BC=2PA=2PB=4,E、F分别是AC、BC的中点.
在三棱锥P-ABC中,PA、PB、PC两两垂直,AC=BC=2PA=2PB=4,E、F分别是AC、BC的中点.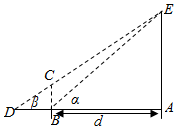 为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题:
为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题: