题目内容

已知点A在抛物线y2=2x上，且到焦点F与到点B（2，1）的距离之和最小，则点A的坐标为
(
1
2
，1)
(
1
2
，1)
．
分析：利用抛物线的定义和三角形三边的大小关系即可得出．
解答：解：过点A作AM⊥准线l，M为垂足，则|AF|=|AM|．
∴|AF|+|AB|=|AM|+|AB|≥|BM|
∴当BA∥x轴时，AF|+|AB|取得最小值|BM|．
把y=1代入抛物线y2=2x，解得x=
1
2
．
∴点A的坐标为(
1
2
，1)．
故答案为(
1
2
，1)．
点评：熟练掌握抛物线的定义和三角形三边的大小关系是解题的关键．
练习册系列答案
相关题目
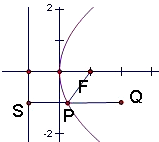精英家教网已知点P在抛物线y2=4x上，那么点P到点Q（2，-1）的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为（　　）
A、(
1
4
，-1)
B、(
1
4
，1)
C、（1，2）
D、（1，-2）
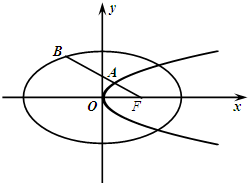精英家教网已知椭圆C：
x2
a2
+
y2
b2
=1的离心率e=
2
2
，且右焦点F到左准线的距离为3．
（1）求椭圆C的方程；
（2）又已知点A为抛物线y2=2px（p＞0）上一点，直线FA与椭圆C的交点B在y轴的左侧，且满足
AB
=2
FA
，求p的最大值．
已知平面上两定点C（-1，0），D（1，0）和一定直线l：x=-4，P为该平面上一动点，作PQ⊥l，垂足为Q，且(
PQ
+2
PC
)•(
PQ
-2
PC
)=0．
（1）问点P在什么曲线上，并求出曲线的轨迹方程M；
（2）又已知点A为抛物线y2=2px（p＞0）上一点，直线DA与曲线M的交点B不在y轴的右侧，且点B不在x轴上，并满足
AB
=2
DA
，求p的最小值．
已知点P在抛物线y2=4x上，则点P到直线l1：4x-3y+6=0的距离和到直线l2：x=-1的距离之和的最小值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网