Question

已知点P在抛物线y²=4x上，那么点P到点Q（2，-1）的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为（　　）

• A、(

  1

  4

  ，-1)
• B、(

  1

  4

  ，1)
• C、（1，2）
• D、（1，-2）

Answer 1

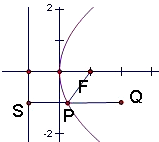
分析：先判断点Q与抛物线的位置，即点Q在抛物线内，再由点P到抛物线焦点距离等于点P到抛物线准线距离，根据图象知最小值在S，P，Q三点共线时取得，可得到答案．

解答：解：点P到抛物线焦点距离等于点P到抛物线准线距离，如图PF+PQ=PS+PQ，故最小值在S，P，Q三点共线时取得，此时P，Q的纵坐标都是-1，
故选A．

点评：本题主要考查抛物线的定义，即抛物线是到定点的距离等于定直线的距离的点的集合．