题目内容
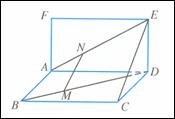 如图,已知矩形
如图,已知矩形![]() 和矩形
和矩形![]() 所在平面互相垂直,点
所在平面互相垂直,点![]() ,
,![]() 分别在对角线
分别在对角线![]() ,
,![]() 上,且
上,且![]() ,
,![]() .求证:
.求证:![]() 平面
平面![]() .
.
解析:要证明![]() 平面
平面![]() ,只要证明向量
,只要证明向量![]() 可以用平面
可以用平面![]() 内的两个不共线的向量
内的两个不共线的向量![]() 和
和![]() 线性表示.
线性表示.
答案:证明:如图,因为![]() 在
在![]() 上,且
上,且![]() ,所以
,所以![]() .同理
.同理![]() ,又
,又![]() ,所以
,所以![]()
![]()
![]()
![]() .又
.又![]() 与
与![]() 不共线,根据共面向量定理,可知
不共线,根据共面向量定理,可知![]() ,
,![]() ,
,![]() 共面.由于
共面.由于![]() 不在平面
不在平面![]() 内,所以
内,所以![]() 平面
平面![]() .
.
点评:空间任意的两向量都是共面的.与空间的任两条直线不一定共面要区别开.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,已知矩形ABCD,PA⊥面ABCD,M,N分别是AB,PC的中点,PB⊥BC(注:如果一条直线垂直于平面内任何一条直线,那么称这条直线垂直于这个平面)
如图,已知矩形ABCD,PA⊥面ABCD,M,N分别是AB,PC的中点,PB⊥BC(注:如果一条直线垂直于平面内任何一条直线,那么称这条直线垂直于这个平面)

 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
, ,
,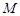 是线段
是线段 的中点.
的中点.
 //平面
//平面 ;
;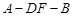 的大小;
的大小;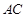 上确定一点
上确定一点 ,使得
,使得 与
与 所成的角是
所成的角是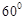 .
.