Question

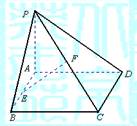
如图，已知矩形ABCD，PA⊥面ABCD，M，N分别是AB，PC的中点，PB⊥BC（注：如果一条直线垂直于平面内任何一条直线，那么称这条直线垂直于这个平面）
（1）证明：MN∥面PAD；
（2）若∠PDA=θ，当θ为何值时，MN和AB，PC都垂直？并说明理由．

Answer 1

分析：（1）取PD的中点E，证明四边形MNEA是平形四边形，可得MN∥AE．再根据直线和平面平行的判定定理证得 MN∥面PAD．
（2）当θ=45°时，MN与AB和PC都垂直．理由：当θ=45°时，证明△ANB为等腰三角形，故有MN⊥AB．同理可证△PMC为等腰三角形，可得MN⊥PC，命题得证．

解答：解：（1）证明：取PD的中点E，连结NE，AE，
∵N分别是PC的中点，则NE为△PCD的中位线，
∴NE∥CD，且NE=

1

2

CD．
再由M为AB的中点，ABCD为矩形，可得AM∥CD，AM=

1

2

CD，
故有 AM∥NE，AM=NE，
所以，四边形MNEA是平形四边形，∴MN∥AE．
又MN?平面PAD，AE?平面PAD，∴MN∥面PAD．
（2）当θ=45°时，MN与AB和PC都垂直．
理由：由于PA⊥面ABCD，当θ=45°时，PA=AD；
∴PA=BC，PB=AC，
连结AN，BN，则有Rt△PAC≌Rt△PBC，∴AN=BN，故△ANB为等腰三角形，∴MN⊥AB．
连结PM、MC，同理可得 Rt△PAM≌Rt△MBC，∴PM=MC，故在等腰PMC中有：MN⊥PC．
从而得到MN和AB，PC都垂直．

点评：本题主要考查直线和平面平行的判定定理，证明两条直线垂直的方法，等腰三角形的性质，属于中档题．