题目内容
如图,底面为正方形的四棱锥S-ABCD 中,P为侧棱SD上的点且SD⊥平面PAC,每条侧棱的长都是底面边长的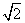 倍.
倍.
(1)求二面角P-AC-D的大小 (2)在侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE:EC的值;若不存在,试说明理由.
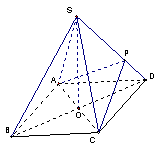
解法一:
(1)连BD,设AC交BD于O,由题意 。在正方形ABCD中,
。在正方形ABCD中,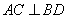 ,所以
,所以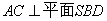 ,得
,得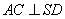 .
.
设正方形边长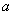 ,则
,则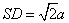 。
。
又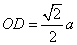 ,所以
,所以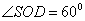 ,
,
连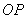 ,知
,知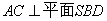 ,所以
,所以 ,
,
且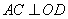 ,所以
,所以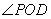 是二面角
是二面角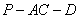 的平面角。
的平面角。
由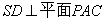 ,知
,知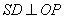 ,所以
,所以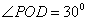 ,
,
即二面角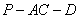 的大小为
的大小为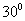 。
。
(2)在棱SC上存在一点E,使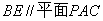
由(1)可得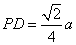 ,故可在
,故可在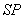 上取一点
上取一点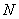 ,使
,使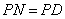 ,过
,过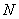 作
作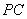 的平行线与
的平行线与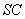 的交点即为
的交点即为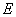 。连BN。在
。连BN。在 中知
中知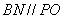 ,又由于
,又由于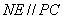 ,故平面
,故平面 ,得
,得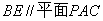 ,由于
,由于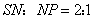 ,故
,故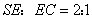 .
.
解析二(1)连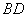 ,设
,设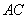 交于
交于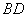 于
于 ,由题意知
,由题意知 .以O为坐标原点,
.以O为坐标原点, 分别为
分别为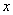 轴、
轴、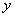 轴、
轴、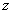 轴正方向,建立坐标系
轴正方向,建立坐标系 如图.
如图.
……………………1分
 设底面边长为
设底面边长为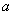 ,则高
,则高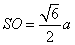 .
.
于是 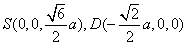 ,
,
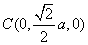 ,
,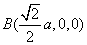

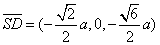 ……………………3分
……………………3分
由题设知,平面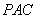 的一个法向量
的一个法向量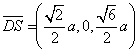 ,平面
,平面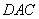 的一个法向量
的一个法向量 ,
,
设所求二面角为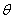 ,则
,则 ,
,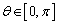
∴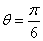 故所求二面角的大小为
故所求二面角的大小为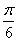 ……………………7分
……………………7分
(2)在棱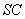 上存在一点
上存在一点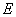 使
使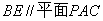 .
.
由(1)知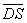 是平面
是平面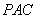 的一个法向量,
的一个法向量,
且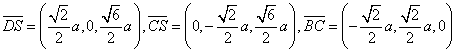
设 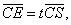 则
则 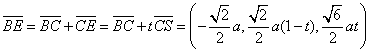
而 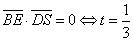
即当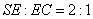 时,
时,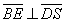


而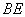 不在平面
不在平面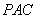 内,故
内,故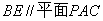 ……………………12分
……………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在 中,
中,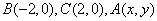 ,给出
,给出 满足的条件,就能得到动点
满足的条件,就能得到动点
的轨迹方程,下表给出了一些条件及方程:
| 条件 | 方程 |
| ① |
|
| ② |
|
| ③ |
|
则满足条件①、②、③的点 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A. 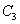 、
、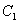 、
、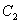 B.
B. 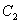 、
、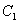 、
、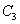
C. 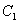 、
、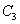 、
、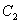 D.
D. 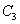 、
、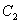 、
、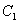
 .设该圆过点
.设该圆过点 的最长弦和最短弦分别为AC和BD,
的最长弦和最短弦分别为AC和BD, B.20
B.20 则
则 .
. 种(用数字作答).
种(用数字作答). 框格内有一块花纹(如图所示),花纹刚好过点
框格内有一块花纹(如图所示),花纹刚好过点 ,经研究发现花纹边界是函数
,经研究发现花纹边界是函数 与
与 图象的一部分,现任取一个点
图象的一部分,现任取一个点 ,则点
,则点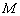 取自阴影部分的概率为 . .
取自阴影部分的概率为 . . ,都有
,都有 ”的否定为
”的否定为 B. 对任意的
B. 对任意的
 ,使
,使



 的导数
的导数
 B.
B.  C.
C.  D.
D. 
 ,若
,若 成立,则点
成立,则点 在
在