题目内容
若x∈[0,
],则函数y=
sin(2x+
)值域为 .
| π |
| 4 |
| 2 |
| π |
| 4 |
考点:复合三角函数的单调性,正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:由函数的定义域求出2x+
的范围,根据正弦函数的性质求出函数的值域.
| π |
| 4 |
解答:
解:∵x∈[0,
],
∴2x+
∈[
,
],
根据正弦函数的性质得,sin(2x+
)∈[
,1],
则
sin(2x+
)∈[1,
],
∴f(x)的值域是[1,
].
故答案为:[1,
].
| π |
| 4 |
∴2x+
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
根据正弦函数的性质得,sin(2x+
| π |
| 4 |
| ||
| 2 |
则
| 2 |
| π |
| 4 |
| 2 |
∴f(x)的值域是[1,
| 2 |
故答案为:[1,
| 2 |
点评:本题考查了复合正弦函数的值域应用,根据函数的定义域求出ωx+φ的范围,再由正弦函数的性质求出函数的值域,考查了整体思想,属于中档题.

练习册系列答案
相关题目
以下对正弦函数y=sinx的图象描述不正确的是( )
| A、在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同 |
| B、介于直线y=1与直线y=-1之间 |
| C、关于x轴对称 |
| D、与y轴仅有一个交点 |
函数f(x)=2cos(x+
),x∈R的最小正周期为( )
| π |
| 6 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
若某算法框图如图所示,则输出的结果为( )
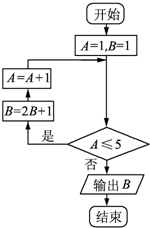

| A、7 | B、15 | C、31 | D、63 |
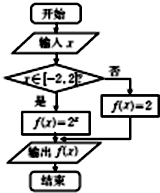 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、[-2,-1] |
| B、(-∞,-1] |
| C、[-1,2] |
| D、[2,+∞) |
 2014年巴西世界杯刚结束,某足球协会为了调查球迷对本届世界杯的了解情况,组织了“世界杯你问我答一百问”活动,该协会从参加活动的球迷(人数不少于1000人)中随机抽取12名球迷.进行世界杯知识问卷测试,测试成绩(百分制)以茎叶图形式表示如右图所示,根据主办方标准.测试成绩低于80分的为“伪球迷”,不低于80分的为“真球迷”.
2014年巴西世界杯刚结束,某足球协会为了调查球迷对本届世界杯的了解情况,组织了“世界杯你问我答一百问”活动,该协会从参加活动的球迷(人数不少于1000人)中随机抽取12名球迷.进行世界杯知识问卷测试,测试成绩(百分制)以茎叶图形式表示如右图所示,根据主办方标准.测试成绩低于80分的为“伪球迷”,不低于80分的为“真球迷”. 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=