题目内容
已知数列{an}满足a1=0,an+1= (n∈N*),则a20等于( )
(n∈N*),则a20等于( )
| A.0 | B.- |
C. | D.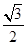 |
B
解析试题分析:根据题意,由于数列{an}满足a1=0,an+1= ,那么可知∴a1=0,a2=-
,那么可知∴a1=0,a2=-
,a3= ,a4=0,a5=-
,a4=0,a5=- ,a6=
,a6= …,故可知数列的周期为3,那么可知a20等于=a2=-
…,故可知数列的周期为3,那么可知a20等于=a2=- ,选B.
,选B.
考点:数列的周期性
点评:本题主要考查学生的应变能力和不完全归纳法,可能大部分人都想直接求数列的通项公式,然后求解,但是此方法不通,很难入手.属于易错题型

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知等差数列 中,
中,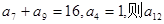 的值是( )
的值是( )
A.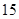 | B. | C.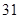 | D.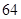 |
设{an}为递增等差数列,前三项的和为12,前三项的积为48,则它的首项为
| A.1 | B.2 | C.4 | D.6 |
在等差数列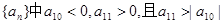 ,数列
,数列 的前
的前 项和为
项和为 ,则在
,则在 中最小的负数为 ( )
中最小的负数为 ( )
A.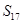 | B.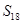 | C.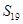 | D.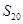 |
数列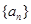 满足
满足 ,且
,且 ,则
,则
 ( ).
( ).
| A.29 | B.28 | C.27 | D.26 |
等差数列{an} 中,a3 =2,则该数列的前5项的和为
| A.10 | B.16 | C.20 | D.32 |
等差数列 的前n项和为
的前n项和为 ,且满足
,且满足 ,则下列数中恒为常数的是( )
,则下列数中恒为常数的是( )
A. | B. | C. | D. |
 ,且对任意的正整数m,n,都有am+n= am + an,则
,且对任意的正整数m,n,都有am+n= am + an,则 等于( )
等于( )

 满足:
满足: ,公差
,公差 . 若当且仅当
. 若当且仅当 时,数列
时,数列 项和
项和 取得最大值,则首项
取得最大值,则首项 的取值范围是( )
的取值范围是( )


