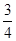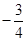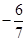题目内容
数列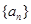 满足
满足 ,且
,且 ,则
,则
 ( ).
( ).
| A.29 | B.28 | C.27 | D.26 |
A
解析试题分析:因为 ,且
,且 ,所以,
,所以, ,故选A。
,故选A。
考点:本题主要考查数列的递推公式,“累加法”,等差数列的求和。
点评:简单题,由 ,且
,且 ,可以逐项求出其它项。也利用“累加法”先求通项公式。
,可以逐项求出其它项。也利用“累加法”先求通项公式。

练习册系列答案
相关题目
类比“等差数列的定义”给出一个新数列“等和数列的定义”是( )
| A.连续两项的和相等的数列叫等和数列 |
| B.从第二项起,以后每一项与前一项的差都不相等的数列叫等和数列 |
| C.从第二项起,以后每一项与前一项的和都相等的数列叫等和数列 |
| D.从第一项起,以后每一项与前一项的和都相等的数列叫等和数列 |
数列 中,a1=-6,且a n+1 =an+ 3,则这个数列的第30项为( )
中,a1=-6,且a n+1 =an+ 3,则这个数列的第30项为( )
| A.81 | B.1125 | C.87 | D.99 |
已知数列{an}满足a1=0,an+1= (n∈N*),则a20等于( )
(n∈N*),则a20等于( )
| A.0 | B.- |
C. | D.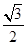 |
等差数列{an}和{bn}的前n项和分别为Sn和Tn,且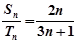 ,则
,则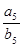 ( )
( )
A.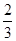 | B.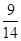 | C.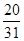 | D.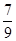 |
等差数列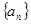 前
前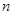 项和为
项和为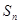 ,
,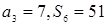 ,则公差d的值为
,则公差d的值为
| A.2 | B.3 | C.-3 | D.4 |
已知等差数列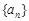 公差
公差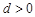 ,前n项和为
,前n项和为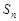 .则“
.则“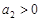 ”是“数列
”是“数列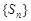 为递增数列”的
为递增数列”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充也不必要条件 |
已知等差数列 中,前
中,前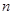 项和为
项和为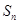 ,若
,若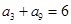 ,则
,则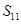 等于( )
等于( )
| A.12 | B.33 | C.66 | D.11 |
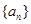 中,
中,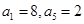 ,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )
,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )