题目内容
19.函数f(x)=$\frac{2x+3}{1+x}$(x>0)的值域是(2,3).分析 分离常数法可得f(x)=2+$\frac{1}{x+1}$,从而解得.
解答 解:f(x)=$\frac{2x+3}{1+x}$=2+$\frac{1}{x+1}$,
∵x>0,∴0<$\frac{1}{x+1}$<1,
∴2+$\frac{1}{x+1}$∈(2,3),
故答案为:(2,3).
点评 本题考查了分离常数法在求函数的值域中的应用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
7.若等比数列{an}的前项和为Sn,且$\frac{{s}_{10}}{{s}_{20}}$=$\frac{2}{3}$,则$\frac{{s}_{20}}{{s}_{40}}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{4}$ |
11.如图,函数的图象在P点处的切线方程是y=-x+8,若点P的横坐标是5,则f(5)+f′(5)=( )
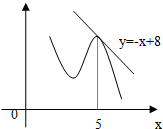

| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 0 |