题目内容
(本小题满分15分)
已知曲线 ,若按向量
,若按向量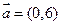 作平移变换得曲线
作平移变换得曲线 ;若将曲线
;若将曲线 按伸缩系数
按伸缩系数 向着
向着 轴作伸缩变换,再按伸缩系数3向着
轴作伸缩变换,再按伸缩系数3向着 轴作伸缩变换得到曲线
轴作伸缩变换得到曲线
(1)求曲线 及
及 方程;
方程;
(2)若 为
为 上一点,
上一点, 为
为 上任意一点,且
上任意一点,且 与曲线
与曲线 相切(
相切( 为切点),
为切点),
求线段 的最大值及对应的
的最大值及对应的 点坐标.
点坐标.
已知曲线
 ,若按向量
,若按向量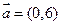 作平移变换得曲线
作平移变换得曲线 ;若将曲线
;若将曲线 按伸缩系数
按伸缩系数 向着
向着 轴作伸缩变换,再按伸缩系数3向着
轴作伸缩变换,再按伸缩系数3向着 轴作伸缩变换得到曲线
轴作伸缩变换得到曲线
(1)求曲线
 及
及 方程;
方程;(2)若
 为
为 上一点,
上一点, 为
为 上任意一点,且
上任意一点,且 与曲线
与曲线 相切(
相切( 为切点),
为切点),求线段
 的最大值及对应的
的最大值及对应的 点坐标.
点坐标.



(1)设曲线 上任意一点
上任意一点 ,
,
经变换后曲线 上对应点
上对应点 ,设经变换后曲线
,设经变换后曲线 上对应点
上对应点
则由题知 则
则 代入曲线
代入曲线 得
得
故曲线 的方程为
的方程为 .o. ………….3分m
.o. ………….3分m
又 ,则
,则 代入曲线
代入曲线 得
得
故曲线 的方程为
的方程为 .o. ………….6分m
.o. ………….6分m
(2)设 ,经分析知要想
,经分析知要想 最大,即
最大,即 到圆心距离
到圆心距离 最大…….7分m
最大…….7分m
即
 =
= =
= .o……...9分m
.o……...9分m
由 知
知 ,即
,即 , .o. ………….11分m
, .o. ………….11分m
此时 ,故
,故 .o. ………….13分m
.o. ………….13分m
从而 .o. ………….15分m
.o. ………….15分m
 上任意一点
上任意一点 ,
,经变换后曲线
 上对应点
上对应点 ,设经变换后曲线
,设经变换后曲线 上对应点
上对应点
则由题知
 则
则 代入曲线
代入曲线 得
得
故曲线
 的方程为
的方程为 .o. ………….3分m
.o. ………….3分m又
 ,则
,则 代入曲线
代入曲线 得
得
故曲线
 的方程为
的方程为 .o. ………….6分m
.o. ………….6分m(2)设
 ,经分析知要想
,经分析知要想 最大,即
最大,即 到圆心距离
到圆心距离 最大…….7分m
最大…….7分m即
 =
= =
= .o……...9分m
.o……...9分m由
 知
知 ,即
,即 , .o. ………….11分m
, .o. ………….11分m此时
 ,故
,故 .o. ………….13分m
.o. ………….13分m从而
 .o. ………….15分m
.o. ………….15分m
练习册系列答案
相关题目
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 轴,若
轴,若 为双曲线的一条斜率大于0的渐近线,则
为双曲线的一条斜率大于0的渐近线,则



 ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. 相切,且过定点F(1, 0),动圆圆心为M.
相切,且过定点F(1, 0),动圆圆心为M. (O为坐标原点),求证:直线l过一定点.
(O为坐标原点),求证:直线l过一定点.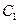 :
: 经过椭圆
经过椭圆 :
: 的两个焦点.
的两个焦点.
 ,又
,又 为
为 轴上的两个交点,若
轴上的两个交点,若 的重心在抛物线
的重心在抛物线 且与直线
且与直线 相切.
相切. 与轨迹E交于点A、B,M是线段AB的中点,过M作
与轨迹E交于点A、B,M是线段AB的中点,过M作 轴的垂线交轨迹E于N.
轴的垂线交轨迹E于N. 与AB平行;
与AB平行; ,使
,使 ?若存在,求
?若存在,求 、
、 ,动点
,动点 ,则点
,则点 的轨迹是 ( )
的轨迹是 ( ) 圆
圆  椭圆
椭圆  双曲线
双曲线  抛物线
抛物线 的焦点为
的焦点为 、
、 ,点
,点 在双曲线上且
在双曲线上且 轴,则
轴,则 的距离为 ( )
的距离为 ( )



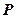 是双曲线
是双曲线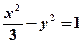 的右支上一动点,F是双曲线的右焦点,已知
的右支上一动点,F是双曲线的右焦点,已知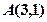 ,则
,则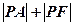 的最小值是 ( )
的最小值是 ( )


