题目内容
3．已知 f（x）=2+1og2x，x∈[1，4]．求y=[f（x）]2-2f（x）的最大值及此时x的值．分析 根据f（x）的定义域为[1，4]先求出y的定义域为[0，2]，然后即可确定y=[f（x）]2-2f（x）的最大值及相应的x的值．
解答 解：y=（2+log2x）2-2（2+log2x）=（log3x+1）2-1
∵1≤x≤4，∴0≤log3x≤2．
∴当x=4时，y=[f（x）]2-2f（x）有最大值8．
点评 本题主要考察了对数函数图象与性质的综合应用，其中根据f（x）的定义域先求出y的定义域是正确解题的关键步骤，属于基础题．
练习册系列答案
相关题目
14．不等式6${\;}^{（{x}^{2}+x-2）}$＜1的解集是（ ）
| A． | （-1，2） | B． | （-2，1） | C． | R | D． | ∅ |
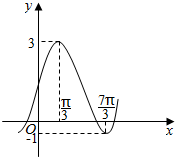已知平面向量$\overrightarrow{a}$=（sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$，cos2$\frac{ωx}{2}$），$\overrightarrow{b}$=（cosφ，sinφ），函数f（x）=2A（$\overrightarrow{a}$•$\overrightarrow{b}$）-Asinφ+k（其中A＞0，|φ|＜$\frac{π}{2}$）的图象如图所示．
18．f（x）=ax2+bx+c满足f（0）=3，对称轴是直线x=-1，最小值为2，则该函数的表达式为（ ）
| A． | f（x）=x2-2x-3 | B． | f（x）=x2+2x-3 | C． | f（x）=x2-2x+3 | D． | f（x）=x2+2x+3 |
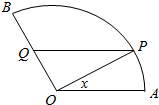如图，准备在扇形空地AOB上修建一个山水景观OPQ，己知∠AOB=$\frac{2}{3}$π，OA=lkm，点P在扇形弧上，PQ∥OA交OB于点Q，记∠POA=x．
在如图所示的表格中，如果第一格填上一个数后，每一行成等比数列，每一列成等差数列，则x+y+z=2．