题目内容
已知 =(x2+1,p+2),
=(x2+1,p+2), =(3,x).
=(3,x).
(I)当p=8时,若
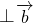 ,求x的值.
,求x的值.
(II)若存在唯一的实数x,使 +
+ 与
与 =(1,2)平行,试求p的值.
=(1,2)平行,试求p的值.
解:(I)当p=8时,由
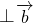 可得
可得  =(x2+1,10)•(3,x)=3x2+3+10x=0,即 (3x+1)(x+3)=0
=(x2+1,10)•(3,x)=3x2+3+10x=0,即 (3x+1)(x+3)=0
解得 x=-3,或 x=- .
.
(II)∵ =(x2+4,p+2+x),
=(x2+4,p+2+x), =(1,2),由
=(1,2),由 +
+ 与
与 =(1,2)平行可得2(x2+4)=p+2+x,即 2x2-x+6-p=0.
=(1,2)平行可得2(x2+4)=p+2+x,即 2x2-x+6-p=0.
由题意可得 判别式△=1-8(6-p)=0,解得 p= .
.
分析:(I)当p=8时,由
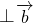 可得
可得  =(x2+1,10)•(3,x)=3x2+3+10x=0,由此求得x的值.
=(x2+1,10)•(3,x)=3x2+3+10x=0,由此求得x的值.
(II)先求出 的坐标,再根据
的坐标,再根据 +
+ 与
与 =(1,2)平行得到 2x2-x+6-p=0,由判别式△=0求得x的值.
=(1,2)平行得到 2x2-x+6-p=0,由判别式△=0求得x的值.
点评:本题主要考查两个向量垂直、共线的性质,数量积公式的应用,属于中档题.

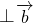 可得
可得  =(x2+1,10)•(3,x)=3x2+3+10x=0,即 (3x+1)(x+3)=0
=(x2+1,10)•(3,x)=3x2+3+10x=0,即 (3x+1)(x+3)=0 解得 x=-3,或 x=-
 .
.(II)∵
 =(x2+4,p+2+x),
=(x2+4,p+2+x), =(1,2),由
=(1,2),由 +
+ 与
与 =(1,2)平行可得2(x2+4)=p+2+x,即 2x2-x+6-p=0.
=(1,2)平行可得2(x2+4)=p+2+x,即 2x2-x+6-p=0.由题意可得 判别式△=1-8(6-p)=0,解得 p=
 .
.分析:(I)当p=8时,由

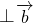 可得
可得  =(x2+1,10)•(3,x)=3x2+3+10x=0,由此求得x的值.
=(x2+1,10)•(3,x)=3x2+3+10x=0,由此求得x的值.(II)先求出
 的坐标,再根据
的坐标,再根据 +
+ 与
与 =(1,2)平行得到 2x2-x+6-p=0,由判别式△=0求得x的值.
=(1,2)平行得到 2x2-x+6-p=0,由判别式△=0求得x的值.点评:本题主要考查两个向量垂直、共线的性质,数量积公式的应用,属于中档题.

练习册系列答案
相关题目
已知曲线y=x2在点P处切线与直线3x-y+1=0的夹角为45°,那么点P坐标为( )
| A、(-1,1) | ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-1,1),(
|
已知双曲线y2-x2=1的离心率为e,且抛物线y2=2px的焦点坐标为(e2,0),则p的值为( )
| A、-2 | B、-4 | C、2 | D、4 |