题目内容
已知双曲线y2-x2=1的离心率为e,且抛物线y2=2px的焦点坐标为(e2,0),则p的值为( )
| A、-2 | B、-4 | C、2 | D、4 |
分析:由双曲线y2-x2=1得a=1,b=1.所以e=
.可得抛物线的焦点坐标既是(e2,0)又是(
,0),所以可得p=4.
| 2 |
| p |
| 2 |
解答:解:由双曲线y2-x2=1得a=1,b=1.所以c=
=
,所以e=
.
所以抛物线的焦点坐标为(2,0).
又因为抛物线y2=2px的焦点坐标为(
,0)
所以p=4.
故选D.
| a2+b2 |
| 2 |
| 2 |
所以抛物线的焦点坐标为(2,0).
又因为抛物线y2=2px的焦点坐标为(
| p |
| 2 |
所以p=4.
故选D.
点评:解决此类问题的关键是熟悉双曲线与抛物线中相关数值之间的关系.

练习册系列答案
相关题目
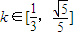 时,求mn的取值范围.
时,求mn的取值范围. 时,求
时,求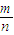 的取值范围.
的取值范围.