题目内容
双曲线 的渐近线与圆
的渐近线与圆 没有公共点,则双曲线离心率的取值范围是
没有公共点,则双曲线离心率的取值范围是
 的渐近线与圆
的渐近线与圆 没有公共点,则双曲线离心率的取值范围是
没有公共点,则双曲线离心率的取值范围是 (1,2)
分析:双曲线
 的渐近线方程是bx±ay=0,圆x2+(y-2)2=1的圆心O(0,2),半径r=1,由双曲线
的渐近线方程是bx±ay=0,圆x2+(y-2)2=1的圆心O(0,2),半径r=1,由双曲线 的渐近线与圆x2+(y-2)2=1没有公共点,知d=
的渐近线与圆x2+(y-2)2=1没有公共点,知d=  >1,由此能求出双曲线离心率的取值范围.
>1,由此能求出双曲线离心率的取值范围.解:双曲线
 的渐近线方程是y=±
的渐近线方程是y=± x,
x,即bx±ay=0,
圆x2+(y-2)2=1的圆心O(0,2),半径r=1,
∵双曲线
 的渐近线与圆x2+(y-2)2=1没有公共点,
的渐近线与圆x2+(y-2)2=1没有公共点,∴圆心O(0,2)到渐近线bx±ay=0的距离:
d=
 >1,
>1,∴
 >1,
>1,∴e=
 <2,
<2,∵e>1,
∴双曲线离心率的取值范围是(1,2).
故答案为:(1,2).

练习册系列答案
相关题目
 -1,m
-1,m 0).
0). , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为 的直线
的直线 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为 ,求证
,求证 为定值;
为定值; ,且
,且 ,求
,求


 且倾斜角为
且倾斜角为 的直线与双曲线交于
的直线与双曲线交于 两点,求线段
两点,求线段 的长。
的长。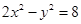 的实轴长是
的实轴长是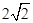
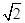
 的渐近线方程为
的渐近线方程为 ,则
,则 的值为( )
的值为( ) 有相同的焦点,它的一条渐近线方程为
有相同的焦点,它的一条渐近线方程为 ,则双曲线的方程为 ( )
,则双曲线的方程为 ( )



 的左焦点为
的左焦点为 ,
, ,当
,当 时,则该双曲线的离心率
时,则该双曲线的离心率 等于 ( )
等于 ( ) 




 的离心率为
的离心率为 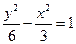 ,则以双曲线中心为顶点,以双曲线准线为准线的抛物线方程为.
,则以双曲线中心为顶点,以双曲线准线为准线的抛物线方程为.