题目内容
7．已知p：x≥m，q：|x-1|＜1，若￢q是￢p的必要不充分条件，则实数m的取值范围是m≤0．分析 求出关于q的不等式，根据￢q是￢p的必要不充分条件，得到（0，2）⊆[m，+∞），求出m的范围即可．
解答 解：p：x≥m，
q：|x-1|＜1，即：q：0＜x＜2，
若￢q是￢p的必要不充分条件，
则p是q的必要不充分条件，
则（0，2）⊆[m，+∞），
则实数m的取值范围是m≤0，
故答案为：m≤0．
点评 本题考查了充分必要条件，考查集合的包含关系，是一道基础题．
练习册系列答案
相关题目
17．以下四个命题中不正确的是 （ ）
| A． | $f（x）=\frac{|x|}{x}$是奇函数 | B． | f（x）=x2，x∈（-3，3]是偶函数 | ||
| C． | f（x）=（x-3）2是非奇非偶函数 | D． | y=x4+x2是偶函数 |
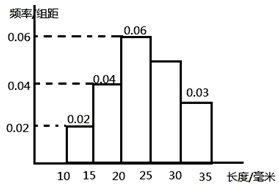对一批产品的长度（单位：mm）进行抽样检测，如图为检测结果的频率分布直方图．根据标准，产品长度在区间[20，25）上的为一等品，在[15，20）和[25，30）上的为二等品，在[10，15）和[30，35）上的为三等品；
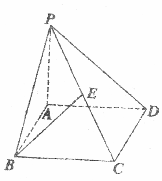如图所示，四棱锥P-ABCD的底面是边长为a的正方形，侧棱PA⊥底面ABCD，在侧面PBC内，有BE⊥PC于E，且BE=$\frac{{\sqrt{6}}}{3}$a．
2．命题p：“?x≥0，e${\;}^{{x}_{0}}$＜x0+1”，则￢p是（ ）
| A． | ?x≥0，ex＜x+1 | B． | ?x≥0，ex＞x+1 | C． | ?x≥0，ex≥x+1 | D． | ?x≥0，ex≥x+1 |
如图，在边长为2的正方形中随机撒1000粒豆子，有180粒落到阴影部分，据此估计阴影部分的面积为0.72．
17．已知sinθ+cosθ=2sinα，sin2θ=2sin2β，则（ ）
| A． | cosβ=2cosα | B． | cos2β=2cos2α | C． | cos2β+2cos2α=0 | D． | cos2β=2cos2α |