Question

已知y=f（x）在（0，+∞）上有意义，且单调递增，并且f（2）=1，f（xy）=f（x）+f（y）.

（1）求证：f（x²）=2f（x）；

（2）求f（1）的值；

（3）若f（x）+f（x+3）≤2，求x的范围.

Answer 1

（1）证明：∵f（xy）=f（x）+f（y），

∴f（x²）=f（x·x）

=f（x）+f（x）

=2f（x）.

（2）解：令x=1，y=2.

f（xy）=f（2）

=f（1）+f（2），

∴f（1）=0.

（3）解：∵f（2）=1，f（4）=f（2²）=2f（2）=2，

∴f（x）+f（x+3）≤2，

得f［x（x+3）］≤f（4）.

由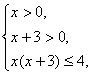

得x∈(0，1].