题目内容
已知y=f(x)在定义域R上是减函数,且f(1-a)<f(2a-1),则a的取值范围是
(-∞,2).
(-∞,2).
.分析:根据函数y=f(x)在定义域R上是减函数,则能推出不等式1-a>2a-1,从而求出a的取值范围.
解答:解:因为y=f(x)在定义域R上是减函数,且f(1-a)<f(2a-1),
使用由减函数的性质可知1-a>2a-1,解得a<2.所以a的取值范围是(-∞,2).
故答案为:(-∞,2).
使用由减函数的性质可知1-a>2a-1,解得a<2.所以a的取值范围是(-∞,2).
故答案为:(-∞,2).
点评:本题考查了函数的单调性的应用,属于基础题型.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
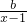 -a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0
-a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0 -a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0
-a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0 -a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0
-a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0