题目内容
已知y=f(x)在定义域(-1,1)上是减函数,且f(1-a)<f(2a-1),则a的取值范围是( )
分析:由f(1-a)<f(2a-1),根据函数的定义域以及函数的单调递减函数的定义自变量小的函数值大进行建立不等关系,解之即可.
解答:解:∵f(x)在定义域(-1,1)上是减函数,且f(1-a)<f(2a-1)
∴
解得0<a<
故选C
∴
|
解得0<a<
| 2 |
| 3 |
故选C
点评:本题主要考查了函数的单调性及单调区间,以及利用单调性求解不等式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
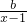 -a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0
-a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0 -a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0
-a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0 -a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0
-a(a∈R,a≠0)在x=3处的切线方程为(2a-1)x-2y+3=0