题目内容
已知函数
(Ⅰ)若 时,函数
时,函数 在其定义域上是增函数,求b的取值范围;
在其定义域上是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设函数 求
求 的最小值;
的最小值;
(Ⅲ)设函数 的图象C1与函数
的图象C1与函数 的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
(I) ;(II)(Ⅲ)见解析;
;(II)(Ⅲ)见解析;
【解析】
试题分析:(1)依题意: ∵
∵ 上是增函数∴
上是增函数∴ 对
对 恒成立,又
恒成立,又 故b的取值范围为
故b的取值范围为 (2)设
(2)设 ,则
,则 ,即
,即
 ,这里需分三类讨论第一类
,这里需分三类讨论第一类 第二类
第二类 第三类
第三类 (3)设点P、Q的坐标是
(3)设点P、Q的坐标是 假设C1在点M处的切线与C2在点N处的切线平行,则
假设C1在点M处的切线与C2在点N处的切线平行,则 即
即 则
则




 ,
, ,再通过构造新函数推出矛盾
,再通过构造新函数推出矛盾
试题解析:(1)依题意: ∵
∵ 上是增函数,
上是增函数,
∴ 对
对 恒成立, 2分
恒成立, 2分
∴ ∵
∵
 ∴b的取值范围为
∴b的取值范围为 4分
4分
(2)设 ,则
,则 ,即
,即
 5分
5分
∴当 即
即 时函数y在[1,2]上为增函数,
时函数y在[1,2]上为增函数,
当t=1时, 6分
6分
当 即
即 时,
时, 7分
7分
当 即
即 时,函数y在[1,2]上为减函数,
时,函数y在[1,2]上为减函数,
当t=2时, 8分
8分
综上所述,当 时
时 的最小值为b+1
的最小值为b+1
当 时
时 的最小值为
的最小值为
当 时
时 的最小值为4+2b 9分
的最小值为4+2b 9分
(3)设点P、Q的坐标是 则点M、N的横坐标为
则点M、N的横坐标为
C1在M处的切线斜率为 C2在点N处的切线斜率
C2在点N处的切线斜率
假设C1在点M处的切线与C2在点N处的切线平行,则
即
则



 ,
, 12分
12分
设 ①
①
令 则
则
∵ ∴
∴
所以 上单调递增,故
上单调递增,故 , 则
, 则
这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行. 14分
考点:导数的综合应用

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 .
.




 的一个焦点在圆
的一个焦点在圆 上,则双曲线的渐近线方程为
上,则双曲线的渐近线方程为 B.
B. C.
C. D.
D.
 中,
中, ,
, 则数列
则数列 B.
B. C.
C. D.
D.
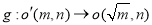
 ,现有点
,现有点 与
与 ,点
,点 是线段
是线段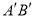 上一动点,按定义的对应法则
上一动点,按定义的对应法则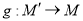 ,当点
,当点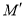 在线段
在线段 上从点的
上从点的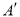 开始运动到点
开始运动到点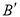 结束时,则点
结束时,则点 的对应点
的对应点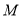 所形成的轨迹与x轴围成的面积为
所形成的轨迹与x轴围成的面积为  的渐近线与抛物线
的渐近线与抛物线 相切,则该双曲线的离心率等于 ( )
相切,则该双曲线的离心率等于 ( ) B.
B. C.
C. D.
D.
 中,
中, ,
, ,
, ,
, ,梯形所在平面内一点
,梯形所在平面内一点 满足
满足 ,则
,则 .
. 中,
中, ,以
,以 为直径的圆
为直径的圆 交
交 于点
于点 ,点
,点 是
是 边的中点,连接
边的中点,连接 交圆
交圆 于点
于点 .
.
 是圆
是圆 .
.