题目内容
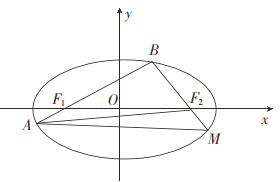
【题目】已知椭圆![]() :
:![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的长轴长与焦距之比为
的长轴长与焦距之比为![]() ,过
,过![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积;
的面积;
(2)若在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 是以
是以![]() 为顶点的等腰三角形,求直线
为顶点的等腰三角形,求直线![]() 的方程.
的方程.
【答案】(1)12(2)![]()
【解析】
(1)结合椭圆的基本性质,分别计算a,b,c的值,代入直线方程,即可。(2)代入直线方程,结合等腰三角形底边和高相互垂直,建立等式,计算k,得到直线l的方程,即可。
解:(1)依题意,因![]() ,又
,又![]() ,得
,得![]() ,
,![]()
所以椭圆![]() 的方程为
的方程为![]() ,
,
设![]() 、
、![]() ,当
,当![]() 时,直线
时,直线![]() :
:![]()
将直线与椭圆方程联立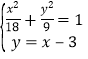 ,
,
消去![]() 得,
得,![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,
所以![]()
![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() ,由题意可知
,由题意可知![]() ,
,
由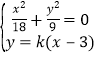 ,消去
,消去![]() 得,
得,![]() ,
,
![]() 恒成立,
恒成立,![]() ,线段
,线段![]() 的中点
的中点![]() ,
,
则![]() ,
,![]() ,
,
若![]() 是以
是以![]() 为顶点的等腰三角形,则
为顶点的等腰三角形,则![]() ,得
,得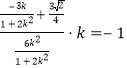 ,
,
整理得:![]() .故直线
.故直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目