题目内容
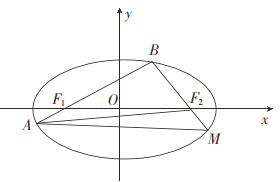
【题目】已知椭圆
的左、右焦点分别为
，
，过点
的直线与椭圆
交于
两点，延长
交椭圆于点
，
的周长为8.
（1）求的离心率及方程；
（2）试问：是否存在定点
，使得
为定值？若存在，求
；若不存在，请说明理由.
【答案】（1）
,
； （2）存在点
，且
.
【解析】
（1）由已知条件得
，
，即可计算出离心率和椭圆方程
（2）假设存在点，分别求出直线
的斜率不存在、直线的斜率存在的表达式，令其相等，求出结果
（1）由题意可知，
，则，
又
的周长为8，所以
，即，
则
，
.
故
的方程为.
（2）假设存在点，使得
为定值.
若直线的斜率不存在，直线的方程为
，
，
，
则
.
若直线的斜率存在，设的方程为
，
设点
，
，联立
，得
，
根据韦达定理可得：
，
，
由于
，
，
则
因为为定值，所以
，
解得，故存在点，且.
练习册系列答案
相关题目
【题目】一商场对5年来春节期间服装类商品的优惠金额
（单位：万元）与销售额
（单位：万元）之间的关系进行分析研究并做了记录，得到如下表格.
日期 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图，并判断服装类商品的优惠金额与销售额是正相关还是负相关；
(2)根据表中提供的数据，求出与的回归方程
；
(3)若2019年春节期间商场预定的服装类商品的优惠金额为10万元，估计该商场服装类商品的销售额.
参考公式：
参考数据：
