题目内容
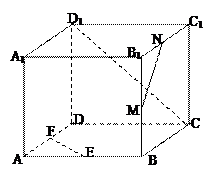
在长方体ABCD—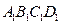 中,AB=2,
中,AB=2,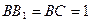 ,E为
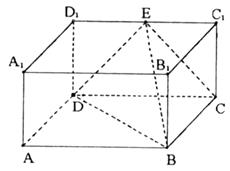
,E为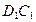 的中点,连结ED,EC,EB和DB,
的中点,连结ED,EC,EB和DB,
(1)求证:平面EDB⊥平面EBC;
(2)求二面角E-DB-C的正切值.
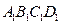 中,AB=2,
中,AB=2,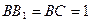 ,E为
,E为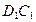 的中点,连结ED,EC,EB和DB,
的中点,连结ED,EC,EB和DB,(1)求证:平面EDB⊥平面EBC;
(2)求二面角E-DB-C的正切值.
 |
(1)见解析(2)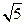
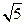
(1)证明:在长方体ABCD-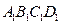 中,AB=2,
中,AB=2,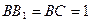 ,E为
,E为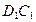 的中点。
的中点。
∴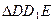 为等腰直角三角形,
为等腰直角三角形,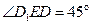 。
。
同理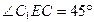 。
。
∴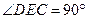 ,即DE⊥EC。
,即DE⊥EC。
在长方体ABCD-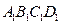 中,BC⊥平面
中,BC⊥平面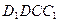 ,又DE
,又DE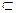 平面
平面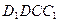 ,
,
∴BC⊥DE。
又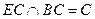 ,∴DE⊥平面EBC。∵平面DEB过DE,
,∴DE⊥平面EBC。∵平面DEB过DE,
∴平面DEB⊥平面EBC。
(2)解:如图,过E在平面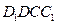 中作EO⊥DC于O。
中作EO⊥DC于O。
在长方体ABCD-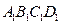 中,∵面ABCD⊥面
中,∵面ABCD⊥面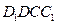 ,
,
∴EO⊥面ABCD。过O在平面DBC中作OF⊥DB于F,连结EF
∴EF⊥BD。∠EFO为二面角E-DB-C的平面角。
利用平几知识可得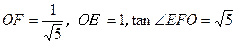
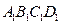 中,AB=2,
中,AB=2,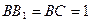 ,E为
,E为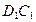 的中点。
的中点。∴
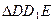 为等腰直角三角形,
为等腰直角三角形,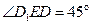 。
。同理
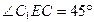 。
。∴
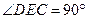 ,即DE⊥EC。
,即DE⊥EC。在长方体ABCD-
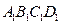 中,BC⊥平面
中,BC⊥平面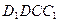 ,又DE
,又DE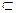 平面
平面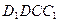 ,
,∴BC⊥DE。
又
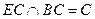 ,∴DE⊥平面EBC。∵平面DEB过DE,
,∴DE⊥平面EBC。∵平面DEB过DE,∴平面DEB⊥平面EBC。
(2)解:如图,过E在平面
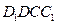 中作EO⊥DC于O。
中作EO⊥DC于O。在长方体ABCD-
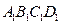 中,∵面ABCD⊥面
中,∵面ABCD⊥面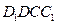 ,
,∴EO⊥面ABCD。过O在平面DBC中作OF⊥DB于F,连结EF
∴EF⊥BD。∠EFO为二面角E-DB-C的平面角。
利用平几知识可得

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
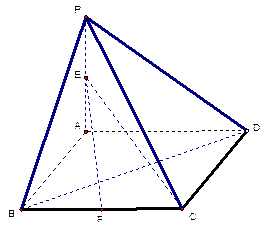
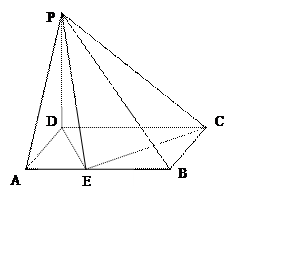 已知PD=
已知PD=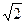 ,CD=2,AE=
,CD=2,AE=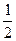 ,
,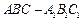 中,
中,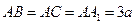 ,
, 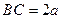 ,
,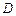 是
是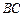 的中点,
的中点,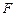 是
是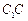 上一点,且
上一点,且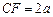 .
.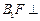 平面
平面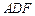 ;
;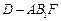 的体积;
的体积;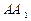 上找一点
上找一点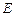 ,使得
,使得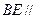 平面
平面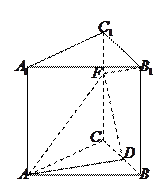
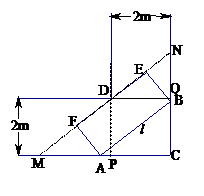
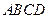 中,底面
中,底面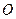 是正方形
是正方形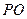
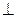 底面
底面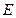 是
是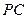 的中点.
的中点.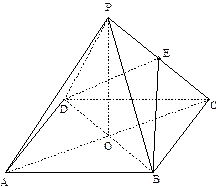
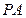 ∥平面
∥平面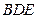 ;
;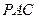
 中,四边形
中,四边形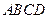 是正方形,
是正方形,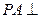 平面
平面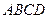 ,
,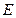 是
是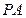 上的一点,
上的一点,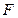 是
是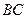 的中点
的中点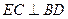 ;
;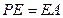 ,求证:
,求证: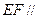 平面
平面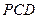 .
.