题目内容
20.下列从集合A到集合B的各对应关系中,为映射的是( )| A. | A={x|-1≤x≤1},B={x|0≤x≤2},f:x→y=|x| | B. | $A=R,B=R,f:x→y=\frac{1}{x}$ | ||
| C. | $A=R,B=R,f:x→y=\left\{\begin{array}{l}0,x≥0\\ 1,x≤0\end{array}\right.$ | D. | $A=N,B=Q,f:x→y=\sqrt{x}+1$ |
分析 根据映射的概念,对于集合A中的任何一个元素在集合B中都有唯一的对应.
解答 解:对于A符合映射的概念,故正确;
对于B,A中的0在B中没有对应,故不正确;
对于C,A中的0在B中有2个对应是0和1,故不正确;
对于D,A中的2在B中没有对应,故不正确.
故选:A.
点评 本题考查映射的定义,对于前一个集合中的任何一个元素在后一个集合中都有唯一确定的元素和它对应,这样的对应才是映射

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
9.如图,在矩形 OABC中,$\overrightarrow{{A}{B}}=3\overrightarrow{{A}{E}}$,$\overrightarrow{{B}C}=3\overrightarrow{FC}$,若$\overrightarrow{{O}{B}}=λ\overrightarrow{{O}{E}}+μ\overrightarrow{{O}F}$(λ,μ∈R),则λμ等于( )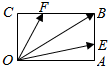

| A. | $\frac{9}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{4}{9}$ | D. | $\frac{16}{9}$ |
 如图,已知斜三棱柱ABC-A1B1C1的侧面ACC1A1与底面ABC垂直,$∠ABC=90°,BC=2,AC=2\sqrt{3},A{A_1}⊥{A_1}C,A{A_1}={A_1}C$.
如图,已知斜三棱柱ABC-A1B1C1的侧面ACC1A1与底面ABC垂直,$∠ABC=90°,BC=2,AC=2\sqrt{3},A{A_1}⊥{A_1}C,A{A_1}={A_1}C$.