题目内容
椭圆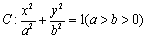 的上顶点为
的上顶点为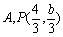 是
是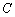 上的一点,以
上的一点,以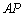 为直径的圆经过椭圆
为直径的圆经过椭圆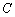 的右焦点
的右焦点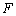 .
.
(1)求椭圆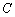 的方程;
的方程;
(2)动直线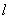 与椭圆
与椭圆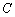 有且只有一个公共点,问:在
有且只有一个公共点,问:在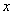 轴上是否存在两个定点,它们到直线
轴上是否存在两个定点,它们到直线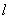 的距离之积等于1?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
的距离之积等于1?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
解析:(1)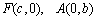 ,由题设可知
,由题设可知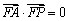 ,得
,得
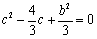 ① ………1分
① ………1分
又点P在椭圆C上,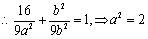 ②
②
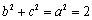 ③ ………3分
③ ………3分
①③联立解得,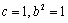 ………4分
………4分
故所求椭圆的方程为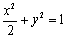 ………5分
………5分
(2)当直线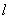 的斜率存在时,设其方程为
的斜率存在时,设其方程为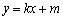 ,代入椭圆方程,消去y,
,代入椭圆方程,消去y,
整理得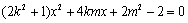 (﹡)
(﹡)
方程(﹡)有且只有一个实根,又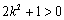 ,
,
所以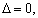 得
得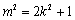 ………8分
………8分
假设存在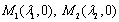 满足题设,则由
满足题设,则由
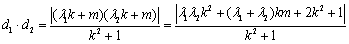
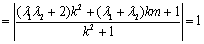 对任意的实数
对任意的实数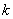 恒成立,
恒成立,
所以, 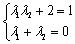 解得,
解得,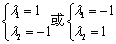
当直线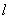 的斜率不存在时,经检验符合题意.
的斜率不存在时,经检验符合题意.
总上,存在两个定点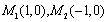 ,使它们到直线
,使它们到直线 的距离之积等于1.…12分
的距离之积等于1.…12分
【思路点拨】(1)由题设可得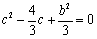 ①,又点P在椭圆C上,可得
①,又点P在椭圆C上,可得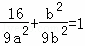 ⇒a2=2②,又b2+c2=a2=2③,①③联立解得c,b2,即可得解.
⇒a2=2②,又b2+c2=a2=2③,①③联立解得c,b2,即可得解.
(2)设动直线l的方程为y=kx+m,代入椭圆方程消去y,整理得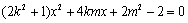 (﹡),由
(﹡),由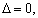 得
得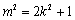 ,假设存在
,假设存在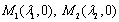 满足题设,则由
满足题设,则由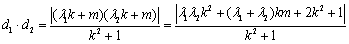
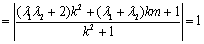 对任意的实数k恒成立.由
对任意的实数k恒成立.由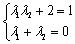 即可求出这两个定点的坐标.
即可求出这两个定点的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的展开式中含有常数项,则
的展开式中含有常数项,则 的最小值等于
的最小值等于 B.
B. C.
C. D.
D.
 ,若方程
,若方程 恰有四个不相等的实数根,则实数
恰有四个不相等的实数根,则实数 的取值范围是____________.
的取值范围是____________. ,则复数
,则复数 ()
() B.
B. C.
C. D.
D.



 ,
, ,则
,则 =( )
=( ) (B)
(B) (C)
(C) (D)
(D)
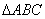 中,角
中,角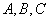 所对的边分别为
所对的边分别为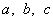 ,满足
,满足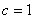 ,
,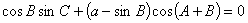 .
.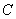 的大小;
的大小;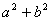 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角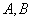 的值.
的值.