题目内容
已知实数x满足4x-10•2x+16≤0,求函数 的值域.
的值域.
解:由题意知:4x-10•2x+16≤0,解得2≤2x≤8,
∴1≤x≤3,
∵ =
= ,
,
令t=log3x,则t∈[0,1],
∴y=t2- t+2=(t-
t+2=(t- )2+
)2+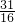 ,t∈[0,1],
,t∈[0,1],
∴当t= 时,ymin=
时,ymin=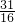 ,
,
当t=1时,ymax= ,
,
∴f(x)的值域是 .
.
分析:把“指数2x”作为一个整体,求不等式(2x)2-10•2x+16≤0的解集,即可求出log3x的范围,利用换元法化简函数的解析式为y=t2- t+2,转化为二次函数利用配方法即可求出函数的值域.
t+2,转化为二次函数利用配方法即可求出函数的值域.
点评:本题考查了求指数型的不等式和对数型复合函数的值域,把“对数log3x”作为一个整体,求它的范围,利用对数的运算把函数转化为关于它的二次函数,利用二次函数的性质求函数的值域,考查了整体思想和转化思想,属中档题.
∴1≤x≤3,
∵
 =
= ,
,令t=log3x,则t∈[0,1],
∴y=t2-
 t+2=(t-
t+2=(t- )2+
)2+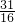 ,t∈[0,1],
,t∈[0,1],∴当t=
 时,ymin=
时,ymin=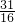 ,
,当t=1时,ymax=
 ,
,∴f(x)的值域是
 .
.分析:把“指数2x”作为一个整体,求不等式(2x)2-10•2x+16≤0的解集,即可求出log3x的范围,利用换元法化简函数的解析式为y=t2-
 t+2,转化为二次函数利用配方法即可求出函数的值域.
t+2,转化为二次函数利用配方法即可求出函数的值域.点评:本题考查了求指数型的不等式和对数型复合函数的值域,把“对数log3x”作为一个整体,求它的范围,利用对数的运算把函数转化为关于它的二次函数,利用二次函数的性质求函数的值域,考查了整体思想和转化思想,属中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目