题目内容
已知函数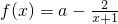 .
.
(1)当a=4,解不等式f(x)>3x;
(2)若函数g(x)=f(2x)是奇函数,求a的值;
(3)若不等式f(x)<x在[0,+∞)上恒成立,求实数a的取值范围.
解:(1)当a=4时,不等式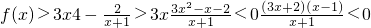
解得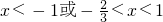 ,
,
∴原不等式的解集为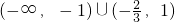 .
.
(2)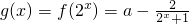 ,∵g(x)是奇函数,∴g(-x)+g(x)=0恒成立.
,∵g(x)是奇函数,∴g(-x)+g(x)=0恒成立.
∴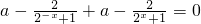 ,
,
即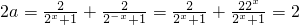 ,∴a=1.
,∴a=1.
(3)f(x)<x在x∈[0,+∞)上恒成立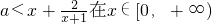 上恒成立,
上恒成立,
设 ,则只需a<h(x)min.
,则只需a<h(x)min.
∵x≥0,∴x+1≥1,∴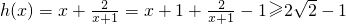 ,
,
当且仅当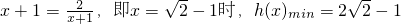 ,
,
∴a的取值范围是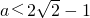 .
.
分析:(1)当a=4时,把要解得不等式等价转化为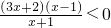 ,由此求得不等式f(x)>3x的解集.
,由此求得不等式f(x)>3x的解集.
(2)由g(x)是奇函数,可得g(-x)+g(x)=0恒成,化简可得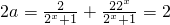 ,从而求得a的值.
,从而求得a的值.
(3)由题意可得 上恒成立,设
上恒成立,设 ,利用基本不等式求得
,利用基本不等式求得 ,从而得到a的取值范围.
,从而得到a的取值范围.
点评:本题主要考查分式不等式的解法,函数的奇偶性的应用以及函数的恒成立问题,体现了化归与转化的数学思想,
属于中档题.
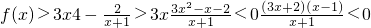
解得
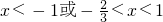 ,
,∴原不等式的解集为
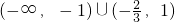 .
.(2)
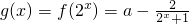 ,∵g(x)是奇函数,∴g(-x)+g(x)=0恒成立.
,∵g(x)是奇函数,∴g(-x)+g(x)=0恒成立.∴
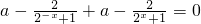 ,
,即
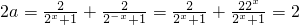 ,∴a=1.
,∴a=1.(3)f(x)<x在x∈[0,+∞)上恒成立
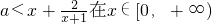 上恒成立,
上恒成立,设
 ,则只需a<h(x)min.
,则只需a<h(x)min.∵x≥0,∴x+1≥1,∴
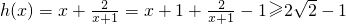 ,
,当且仅当
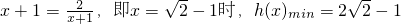 ,
,∴a的取值范围是
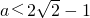 .
.分析:(1)当a=4时,把要解得不等式等价转化为
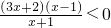 ,由此求得不等式f(x)>3x的解集.
,由此求得不等式f(x)>3x的解集.(2)由g(x)是奇函数,可得g(-x)+g(x)=0恒成,化简可得
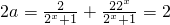 ,从而求得a的值.
,从而求得a的值.(3)由题意可得
 上恒成立,设
上恒成立,设 ,利用基本不等式求得
,利用基本不等式求得 ,从而得到a的取值范围.
,从而得到a的取值范围.点评:本题主要考查分式不等式的解法,函数的奇偶性的应用以及函数的恒成立问题,体现了化归与转化的数学思想,
属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 的极小值;
的极小值; ,x∈[-1,1],求
,x∈[-1,1],求 的最大值F(a).
的最大值F(a). .
. 时,f(x)的值域为[4,6],求a,b的值.
时,f(x)的值域为[4,6],求a,b的值. 函数
函数 .
.