题目内容
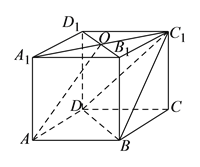
【题目】在四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形,![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.
(I)求证:![]() 平面
平面![]() .
.
(II)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,如果存在,求
,如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
(III)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]() ,求所有满足条件的点
,求所有满足条件的点![]() 构成的图形,并求
构成的图形,并求![]() 的最小值.
的最小值.
【答案】(1)见解析(2)![]() (3)构成的图形是线段
(3)构成的图形是线段![]() ,包括端点,
,包括端点,![]()
【解析】试题分析:(1)由线面垂直得![]() ,由菱形性质得
,由菱形性质得![]() ,再根据线面垂直判定定理得
,再根据线面垂直判定定理得![]() 平面
平面![]() ,(2)连接
,(2)连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 是
是![]() 中点,由平几知识可得
中点,由平几知识可得![]() 是平行四边形,即得
是平行四边形,即得![]() ,再由线面平行判定定理得结论(3)由线面垂直性质与判定定理可得
,再由线面平行判定定理得结论(3)由线面垂直性质与判定定理可得![]() ,即得点
,即得点![]() 构成的图形是线段
构成的图形是线段![]() ,再利用三角形面积求O到直线
,再利用三角形面积求O到直线![]() 距离,即得
距离,即得![]() 的最小值.
的最小值.
试题解析:(I)证明:∵![]() 底面
底面![]() ,
,
∴![]() 底面
底面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 为菱形,
为菱形,
∴![]() ,
,
而![]() ,
,
∴![]() 平面
平面![]() .
.
(II)存在点![]() ,当
,当![]() 是
是![]() 中点,即
中点,即![]() 时,
时,![]() 平面
平面![]() .
.

证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 是
是![]() 中点,
中点,
∵![]() ,且
,且![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴当点![]() 与点
与点![]() 重合时,
重合时,![]() 平面
平面![]() ,
,
此时,![]() .
.
(III)在![]() 内,满足
内,满足![]() 的点构成的图形是线段
的点构成的图形是线段![]() ,包括端点,
,包括端点,
连接![]() ,则
,则![]() ,
,
∵![]() ,
,
∴要使![]() ,只需
,只需![]() ,从而需
,从而需![]() ,
,
又在![]() 中,
中,![]() ,
,
又![]() 为
为![]() 中点,
中点,
∴![]() ,
,
故![]() 点一定在线段
点一定在线段![]() 上,
上,
当![]() 时,
时,![]() 取最小值.
取最小值.
在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]()

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目