题目内容
等比数列{an}的首项a1=1，前n项的和为Sn，若S3=3，则S4=（ ）
| A、-5 | B、-6 |
| C、4或-5 | D、-5或-6 |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：根据等比数列{an}的通项公式与前n项和，求出公比q，再计算S4的值．
解答：
解：等比数列{an}的首项a1=1，S3=3，
∴a1+a2+a3=a1（1+q+q2）=1+q+q2=3，
解得q=1或q=-2；
当q=1时，S4=4a1=4，
当q=-2时，S4=
=-5；
∴S4=4或-5．
故选：C．
∴a1+a2+a3=a1（1+q+q2）=1+q+q2=3，
解得q=1或q=-2；
当q=1时，S4=4a1=4，
当q=-2时，S4=
| a1(1-(-2)4) |
| 1-(-2) |
∴S4=4或-5．
故选：C．
点评：本题考查了等比数列的通项公式与前n项和公式的应用问题，是基础题目．
练习册系列答案
小学课时特训系列答案
相关题目
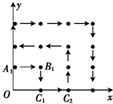为防洪抗旱，某地区大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在A1（0，1）点，第二棵树在B1（1，1）点，第三棵树在C1（1，0）点，第四棵树在C2（2，0）点，接着按图中箭头方向每隔一个单位长度种一棵树，那么，坐标为（43，0）的点是第
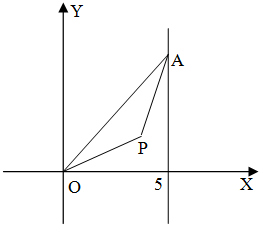如图，点A在直线x=5上移动，等腰△OPA的顶角∠OPA为120°（O，P，A按逆时针方向排列），求点P的轨迹方程．等比数列{an}中，前n项和Sn=
+x，则x的值为（ ）
| 2n |
| 4 |
A、-
| ||
| B、-4 | ||
| C、-1 | ||
| D、4 |
观察下列各数：1，2，2，4，8，32…，则该数列的第8项可能等于（ ）
| A、256 | B、1024 |
| C、4128 | D、8192 |