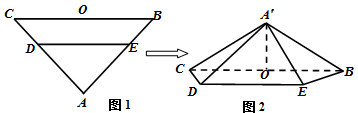
题目内容
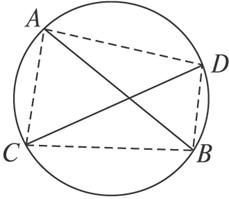
如图2-24,△ABC内接于⊙O,AE切⊙O于点A,BD平分∠ABC,交⊙O于点D,交AF的延长线于点E,DF⊥AE于点F.
图2-24
求证:(1)![]() =
=![]() ;
;
(2)AC =2AF.
思路分析:(1)运用弦切角定理证△ABE∽△DAE即可;(2)依据圆周角定理得点D为![]() 的中点.结合条件容易得到AD平分∠EAC,从而联系“角平分线上的点到角两边距离相等”,过点D作DH⊥AC,垂足为H,结合垂径定理得结论.
的中点.结合条件容易得到AD平分∠EAC,从而联系“角平分线上的点到角两边距离相等”,过点D作DH⊥AC,垂足为H,结合垂径定理得结论.
证明:(1)∵AE切⊙O于点A,∴∠EAD =EBA.?
又∠E =∠E,∴△DAE∽△ABE.?
∴![]() =
=![]() ,即
,即![]() =
=![]() .?
.?
(2)过点D作DH⊥AC,垂足为H.?
∵∠EAD= ∠ABD,∠DAC= ∠DBC,BD平分∠ABC,?
∴∠EAD =∠DAC.又∵DF⊥AE,DH⊥AC,?
∴DF =DH.在Rt△DFA和Rt△DHA中,?
DF =DH,DA= DA,?
∴Rt△DFA≌Rt△DHA.∴AF =AH.?
∵![]() =
=![]() ,DH⊥AC,?
,DH⊥AC,?
∴AH =CH,AC =2AH =2AF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
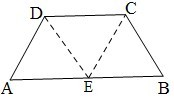 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为( )
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|