题目内容
12.已知指数函数y=f(x)的图象过点($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),则log2f(2)的值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | 2 |
分析 设指数函数y=f(x)=ax(a>0,且a≠1,为常数),把点($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$)代入可得$\frac{\sqrt{2}}{2}$=${a}^{\frac{1}{2}}$,解得a,即可得出.
解答 解:设指数函数y=f(x)=ax(a>0,且a≠1,为常数),
把点($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$)代入可得$\frac{\sqrt{2}}{2}$=${a}^{\frac{1}{2}}$,解得a=$\frac{1}{2}$.
∴$f(x)=(\frac{1}{2})^{x}$,
则log2f(2)=$lo{g}_{2}(\frac{1}{2})^{2}$=-2.
故选:C.
点评 本题考查了指数函数的解析式、指数幂的运算性质、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.若椭圆的两个焦点与其中一个短轴端点恰好连成等腰直角三角形,则该椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{3}$ |
20.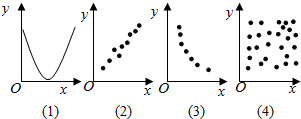 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )
 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (2)(3) |
7.函数$f(x)=\frac{x^2}{{\sqrt{2-x}}}+lg(x+3)$的定义域为( )
| A. | (-3,2] | B. | [-3,2] | C. | (-3,2) | D. | (-∞,-3) |
4.点$(\sqrt{2},\sqrt{3})$在双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)上,且C的焦距为4,则它的离心率为( )
| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |