题目内容
（本小题满分12分）已知函数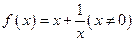
。
（I）判断并证明函数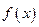
的奇偶性；
（II）判断并证明函数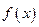在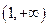
上的单调性；
（III）求函数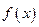在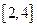
上的最大和最小值。
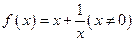。（I）判断并证明函数
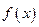的奇偶性；（II）判断并证明函数
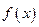在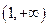上的单调性；（III）求函数
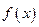在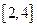上的最大和最小值。解:（Ⅰ）证明:函数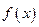的定义域为 x≠0
f(x)=x+
f(-x)=－x+
="-f(x)"
∴函数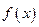是奇函数。…………………4分
（Ⅱ）证明:设 x1
x2∈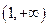， 则f(x1)－f(x2)=(x1-x2)(1-
)
∵x1x2∈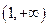 ∴(x1-x2)＜0, (1-)＞0
∴f(x1)－f(x2)0，即f(x1)f(x2).
所以f(x)在定义域R上为增函数. …………………8分
（III）∵f(x)在定义域R上为增函数
∴f(x)的最大值是f(4)=
f(x)的最小值是f(2)=
…………………12分
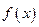的定义域为 x≠0f(x)=x+
f(-x)=－x+="-f(x)" ∴函数
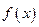是奇函数。…………………4分（Ⅱ）证明:设 x1
x2∈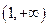， 则f(x1)－f(x2)=(x1-x2)(1-)∵x1
x2∈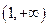 ∴(x1-x2)＜0, (1-)＞0∴f(x1)－f(x2)
0，即f(x1)f(x2).所以f(x)在定义域R上为增函数. …………………8分
（III）∵f(x)在定义域R上为增函数
∴f(x)的最大值是f(4)=
f(x)的最小值是f(2)= …………………12分略
练习册系列答案
相关题目
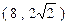，求出函数解析式，并指出函数的单调性与奇偶性。
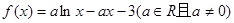
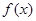的单调区间；
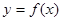的图像在点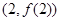
处的切线的斜率为
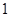，问：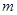 
在什么范围取值时，对于任意的
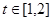，函数
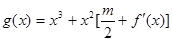在区间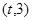
上总存在极值？
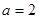时，设函数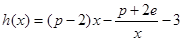
，若在区间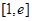
上至少存在一个
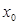，使得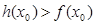
成立，试求实数
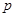的取值范围．
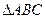的顶点A、B在椭圆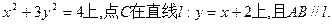
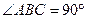，且斜边AC的长最大时，求AB所在直线的方程.
的定义域是__________▲______________.
，
，c
，则（ ）
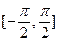上的任意x1、x2,有如下条件：①x1>x2;②|x1|>|x2|;③x13>x23;④x12>x22;⑤|x1|>x2，其中能使f(x1)>f(x2)恒成立的条件的序号是 ；
满足
，且
的导函数
，则
的解集为 
是曲线
上一点，且在点
平行，则点
