题目内容
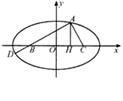
如图所示,B(– c,0),C(c,0),AH⊥BC,垂足为H,且![]() .
.
(1)若![]() = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;
(2)D分有向线段![]() 的比为
的比为![]() ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤![]() ≤
≤![]() 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.
(1)![]() .
.
(2)![]() ≤e≤
≤e≤![]() .
.
解析:
(1)因为![]() ,所以H
,所以H![]() ,又因为AH⊥BC,所以设A
,又因为AH⊥BC,所以设A![]() ,由
,由![]() 得
得![]() 即
即![]() 3分
3分
所以|AB| = ,|AC | =
,|AC | =![]()
椭圆长轴2a = |AB| + |AC| = (![]() + 1)c, 所以,
+ 1)c, 所以,![]() .
.
(2)设D (x1,y1),因为D分有向线段![]() 的比为
的比为![]() ,所以
,所以 ,
,![]() ,
,
设椭圆方程为![]() = 1 (a > b > 0),将A、D点坐标代入椭圆方程得
= 1 (a > b > 0),将A、D点坐标代入椭圆方程得 ![]() .①
.①
![]() …………………………….. ②
…………………………….. ②
由①得![]()
![]() ,代入②并整理得
,代入②并整理得![]() ,
,
因为 – 5≤![]() ≤
≤![]() ,所以
,所以![]() ,又0 < e < 1,所以
,又0 < e < 1,所以![]() ≤e≤
≤e≤![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
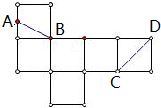 一个正方体的展开图如图所示,B,C,D为原正方体的顶点,A为原正方体一条棱的中点.在原来的正方体中,CD与AB所成角的余弦值为( )
一个正方体的展开图如图所示,B,C,D为原正方体的顶点,A为原正方体一条棱的中点.在原来的正方体中,CD与AB所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
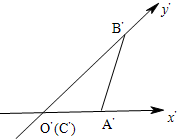 水平放置的△ABC斜二测直观图如图所示,已知A′C′=3,B′C′=2,则△ABC中AB边上中线的实际长度为
水平放置的△ABC斜二测直观图如图所示,已知A′C′=3,B′C′=2,则△ABC中AB边上中线的实际长度为 水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为
水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为 (文)如图所示:已知椭圆C:
(文)如图所示:已知椭圆C: 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为