题目内容
已知△ABC的三个内角A,B,C成等差数列,它们的对边分别为a,b,c,且满足a:b=
:
,c=2.
(Ⅰ)求A,B,C;
(Ⅱ)求△ABC的面积S.
| 2 |
| 3 |
(Ⅰ)求A,B,C;
(Ⅱ)求△ABC的面积S.
考点:正弦定理,余弦定理
专题:三角函数的求值
分析:(Ⅰ)由A,B,C三角成等差数列,利用等差数列的性质及内角和定理求出B的度数,确定出A+C的度数,由a,b,sinB的值,利用正弦定理求出sinA的值,确定出A的度数,进而求出C的度数;
(Ⅱ)利用两角和与差的正弦函数公式及特殊角的三角函数值求出sinC的值,再由sinA,sinB,以及c的值,利用正弦定理求出a与b的值,根据sinC,a,b的值,利用三角形面积公式即可求出三角形ABC面积.
(Ⅱ)利用两角和与差的正弦函数公式及特殊角的三角函数值求出sinC的值,再由sinA,sinB,以及c的值,利用正弦定理求出a与b的值,根据sinC,a,b的值,利用三角形面积公式即可求出三角形ABC面积.
解答:
解:(Ⅰ)∵A,B,C成等差数列,
∴A+C=2B,
又A+B+C=180°,
∴B=60°,A+C=120°,
由正弦定理
=
=
可知,
=
,
∵a:b=
:
,c=2,
∴
=
,即sinA=
,
∵0°<A<120°,
∴A=45°,C=120°-A=75°.
综上,A=45°,B=60°,C=75°;
(Ⅱ)∵sinC=sin75°=sin(30°+45°)=
×
+
×
=
,c=2,sinA=
,sinB=
,
∴由正弦定理得:
=
=
=
,即
=
=
,
整理得:a=2
-2,b=3
-
,
∴S△ABC=
acsinB=
×2(
-1)×2×
=3-
.
∴A+C=2B,
又A+B+C=180°,
∴B=60°,A+C=120°,
由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| a |
| b |
| sinA |
| sinB |
∵a:b=
| 2 |
| 3 |
∴
| ||
|
| sinA |
| sin60° |
| ||
| 2 |
∵0°<A<120°,
∴A=45°,C=120°-A=75°.
综上,A=45°,B=60°,C=75°;
(Ⅱ)∵sinC=sin75°=sin(30°+45°)=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 4 |
| ||
| 2 |
| ||
| 2 |
∴由正弦定理得:
| a |
| sin45° |
| b |
| sin60° |
| c |
| sinC |
| 2 |
| sin75° |
| a | ||||
|
| b | ||||
|
| 2 | ||||||
|
整理得:a=2
| 3 |
| 2 |
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
点评:此题考查了正弦定理,等差数列的性质,以及三角形的面积公式,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
吉安市高二数学竞赛中有一道难题,在30分钟内,学生甲内解决它的概率为
,学生乙能解决它的概率为
,两人在30分钟内独立解决该题,该题得到解决的概率为( )
| 1 |
| 5 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
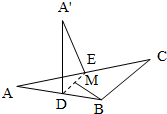 在直角△ABC中,AB=BC=2,D,E分别是AB,AC的中点,将△ADE沿线段DE折起到△A′DE,使平面A′DE⊥平面DBCE,当M是DE的中点时,证明:BM⊥面A′CD.
在直角△ABC中,AB=BC=2,D,E分别是AB,AC的中点,将△ADE沿线段DE折起到△A′DE,使平面A′DE⊥平面DBCE,当M是DE的中点时,证明:BM⊥面A′CD.