题目内容
如果f(n)=1+
+
+
+…+
(n∈N*),那么f(n+1)-f(n)= .
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n |
考点:数列的函数特性
专题:等差数列与等比数列
分析:直接利用已知条件列出关系式,求解即可.
解答:
解:f(n)=1+
+
+
+…+
(n∈N*),
那么f(n+1)-f(n)=1+
+
+
+…+
+
+
-(1+
+
+
+…+
)
=
+
.
故答案为:
+
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n |
那么f(n+1)-f(n)=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n |
=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
故答案为:
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
点评:本题考查数列的函数的特征,数列的通项公式的应用,基本知识的考查.

练习册系列答案
相关题目
某程序框图如图所示,则该程序运行后输出的值是( )


| A、0 | B、2013 |
| C、2014 | D、2015 |
设全集U={1,2,3,4,5,6},集合A={1,2},B={2,3},则A∩(∁UB)=( )
| A、{4,5} | B、{2,3} |
| C、{1} | D、{2} |
 如图,AB是半圆O的直径,C是半圆O上异于A,B的点,CD⊥AB,垂足为D.若AD=2,BC=2
如图,AB是半圆O的直径,C是半圆O上异于A,B的点,CD⊥AB,垂足为D.若AD=2,BC=2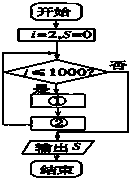 根据条件填空,把求1~1 000内所有偶数的和的程序框图补充完整.①
根据条件填空,把求1~1 000内所有偶数的和的程序框图补充完整.①