题目内容
19.已知两直线l1:(a+1)x-2y+1=0,l2:x+ay-2=0.当a=1时,l1⊥l2.分析 由垂直关系可得a的方程,解方程可得.
解答 解:∵两直线l1:(a+1)x-2y+1=0,l2:x+ay-2=0相互垂直,
∴a+1-2a=0,
解得a=1
故答案为:1
点评 本题考查直线的一般式方程和垂直关系,属基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
3.两个袋中各装有编号为1,2,3,4,5的5个小球,分别从每个袋中摸出一个小球,所得两球编号数之和小于5的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{6}{25}$ | D. | $\frac{2}{5}$ |
7.若函数f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,则下列叙述正确的是( )
| A. | f(x)+g(x)为偶函数 | B. | f(x)g(x)为奇函数 | C. | xf(x)-xg(x)为偶函数 | D. | f(|x|)+xg(x)为奇函数 |
14.已知△ABC的外接圆半径为1,圆心为点O,且$3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=0$,则$\overrightarrow{OC}•\overrightarrow{AB}$的值为( )
| A. | $\frac{8}{5}$ | B. | $\frac{7}{5}$ | C. | $-\frac{1}{5}$ | D. | $\frac{4}{5}$ |
11.对于任意实数a,b,c,d以下四个命题中,其中正确的有( )
①ac2>bc2,则a>b,
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若a>b,则$\frac{1}{a}<\frac{1}{b}$.
①ac2>bc2,则a>b,
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若a>b,则$\frac{1}{a}<\frac{1}{b}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列命题中,正确的是( )
| A. | 若a>b,c>d,则a>c | B. | 若ac>bc,则a>b | ||
| C. | 若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则a<b | D. | 若a>b,c>d,则ac>bd |
9.已知椭圆${C_1}:\frac{x^2}{m^2}+{y^2}=1({m>1})$与双曲线C2:$\frac{{x}^{2}}{{n}^{2}}$-y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则( )
| A. | m>n且e1e2>1 | B. | m>n且e1e2<1 | C. | m<n且e1e2>1 | D. | m<n且e1e2<1 |
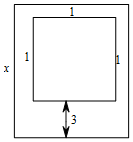 某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?