题目内容
已知函数a＞1，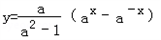
．
（1）判断函数的奇偶性和单调性；
（2）当x∈（﹣1，1）时，有f（1﹣m）+f（1﹣m2）＜0，求m的取值范围．
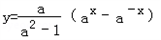．（1）判断函数的奇偶性和单调性；
（2）当x∈（﹣1，1）时，有f（1﹣m）+f（1﹣m2）＜0，求m的取值范围．
解：（1）函数的定义域为R，关于原点对称．
令
，
f（﹣x）=
=﹣f（x），
故函数为奇函数．
由于a＞1，∴
＞0，
函数t=ax在R上是增函数，函数t=﹣
在R上也是增函数，
故
在R上是增函数．
（2）由f（1﹣m）+f（1﹣m2）＜0可得，
f（1﹣m）＜﹣f（1﹣m2）=f（ m2﹣1），
∴1﹣m＜m2﹣1，﹣1＜1﹣m＜1，﹣1＜m2﹣1＜1，
解得1＜m＜
，m的取值范围是（1，
）．
令
，f（﹣x）=
=﹣f（x），故函数为奇函数．
由于a＞1，∴
＞0，函数t=ax在R上是增函数，函数t=﹣
在R上也是增函数，故
在R上是增函数．（2）由f（1﹣m）+f（1﹣m2）＜0可得，
f（1﹣m）＜﹣f（1﹣m2）=f（ m2﹣1），
∴1﹣m＜m2﹣1，﹣1＜1﹣m＜1，﹣1＜m2﹣1＜1，
解得1＜m＜
，m的取值范围是（1，）．
练习册系列答案
相关题目
(a＞1且b＞0).
=
(a＞1).
在（-1，+∞）上为增函数；
=0没有负数根.
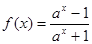(a＞1).
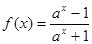(a＞1).