已知圆G:x2+y2—2x—.经过椭圆的右焦点F及上顶点B.过椭圆外一点M的倾斜角为的直线l交椭圆于C.D两点. (Ⅰ)求椭圆方程 (Ⅱ)当右焦点在以线段CD为直径的圆E的内部.求实数m的范围. 题目和参考答案——青夏教育精英家教网—

题目内容

已知圆G：x²+y²—2x—，经过椭圆（a＞b＞0）的右焦点F及上顶点B，过椭圆外一点M（m,0）(m＞0)的倾斜角为的直线l交椭圆于C、D两点.

（Ⅰ）求椭圆方程

（Ⅱ）当右焦点在以线段CD为直径的圆E的内部，求实数m的范围。

（1）2）析】本试题主要是考查了椭圆方程的求解，以及直线与椭圆的位置关系的综合运用。

（1）因为椭圆的离心率为，直线经过椭圆的上顶点和右顶点，并且和圆相切.

结合椭圆的性质和线与圆的位置关系得到参数a,b,c的表达式，得到椭圆的方程。

（2）根据直线方程与椭圆方程联立方程组，结合韦达定理表示出点P的坐标，然后点P在椭圆上得到参数的关系式，，利用m的范围得到op 的范围。

解：（1）由得，所以……………………1分

所以，有，解得………..5分

所以，所以椭圆方程为 …………………………….6分

（2），消去得：

设则，，

故点…………………………………………………9分

点在椭圆上，有，整理得

所以，而，…11分

因为所以，所以，所以…12分

练习册系列答案

相关题目

=1（a＞b＞0）的右焦点F及上顶点B，过圆外一点（m，0）（m＞a）倾斜角为

5π

的直线l交椭圆于C，D两点，
（1）求椭圆的方程；
（2）若右焦点F在以线段CD为直径的圆E的内部，求m的取值范围．

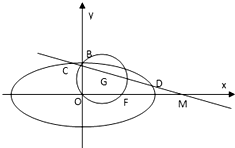如图，已知圆G：x2+y2-2x-

y=0经过椭圆

=1（a＞b＞0）的右焦点F及上顶点B，过椭圆外一点（m，0）（ma）且倾斜角为

π的直线l交椭圆于C，D两点．
（Ⅰ）求椭圆的方程；
（Ⅱ）若

=1(a＞b＞0)的右焦点F及上顶点B．过点M（m，0）作倾斜角为

π的直线l交椭圆于C、D两点．
（1）求椭圆的方程；
（2）若点Q（1，0）恰在以线段CD为直径的圆的内部，求实数m范围．

（2012•虹口区三模）已知圆G：x2+y2-2x-

y=0经过椭圆

=1(a＞b＞0)的右焦点F及上顶点B．
（1）求椭圆的方程；
（2）过椭圆外一点M（m，0）（m＞a）倾斜角为

π的直线l交椭圆于C、D两点，若右焦点F在以线段CD为直径的圆E的外部，求m的取值范围．

已知圆G：x²+y²-2

x-2y=0经过椭圆

=1（a＞b＞0）的右焦点F及上顶点B．
（1）求椭圆的方程；
（2）过椭圆外一点M（m，0）（m＞a）倾斜角为

π的直线l交椭圆于C、D两点，若点N（3，0）在以线段CD为直径的圆E的外部，求m的取值范围．

试题分类