题目内容
 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x-| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 6 |
(Ⅰ)求椭圆的方程;
(Ⅱ)若
| FC |
| FD |
分析:(I)对于圆G:x2+y2-2x-
y=0经过点F,B,分别令y=0,x=0,即可解得F(2,0),B(0,
),可得c=2,b=
.再利用a2=b2+c2即可得到a.
(II)由题意得直线l的方程为y=-
(x-m)(m>
).与椭圆方程联立即可得到根与系数的关系,再利用数量积即可得出.
| 2 |
| 2 |
| 2 |
(II)由题意得直线l的方程为y=-
| ||
| 3 |
| 6 |
解答:解:(1)∵圆G:x2+y2-2x-
y=0经过点F,B,分别令y=0,x=0,
解得F(2,0),B(0,
),
∴c=2,b=
.
∴a2=b2+c2=6.
故椭圆的方程为
+
=1.
(2)由题意得直线l的方程为y=-
(x-m)(m>
).
由
消去y得2x2-2mx+m2-6=0,
由△=4m2-8(m2-6)>0解得-2
<m<2
.
又m>
,∴
<m<2
.
设C(x1,y1),D(x2,y2),则x1+x2=m,x1x2=
.
y1y2=(-
)2(x1-m)(x2-m)=
[x1x2-m(x1+x2)+m2]
∵
=(x1-2,y1),
=(x2-2,y2).
∴
•
=(x1-2)(x2-2)+y1y2=
x1x2-
(x1+x2)+
+4=
.
∵
•
<0,∴
<0.
解得0<m<3,又
<m<2
.
∴
<m<3.
| 2 |
解得F(2,0),B(0,
| 2 |
∴c=2,b=
| 2 |
∴a2=b2+c2=6.
故椭圆的方程为
| x2 |
| 6 |
| y2 |
| 2 |
(2)由题意得直线l的方程为y=-
| ||
| 3 |
| 6 |
由
|
由△=4m2-8(m2-6)>0解得-2
| 3 |
| 3 |
又m>
| 6 |
| 6 |
| 3 |
设C(x1,y1),D(x2,y2),则x1+x2=m,x1x2=
| m2-6 |
| 2 |
y1y2=(-
| ||
| 3 |
| 1 |
| 3 |
∵
| FC |
| FD |
∴
| FC |
| FD |
| 4 |
| 3 |
| m+6 |
| 3 |
| m2 |
| 3 |
| 2m(m-3) |
| 3 |
∵
| FC |
| FD |
| 2m(m-3) |
| 3 |
解得0<m<3,又
| 6 |
| 3 |
∴
| 6 |
点评:本题中考查了椭圆与圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、数量积运算、一元二次不等式的解法等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
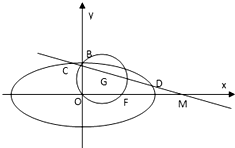 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x- y=0经过椭圆
y=0经过椭圆 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为 的直线l交椭圆于C,D两点,
的直线l交椭圆于C,D两点, ,求m的取值范围。
,求m的取值范围。 
