Question

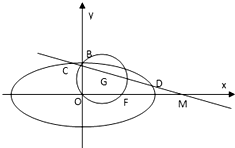如图，已知圆G：x²+y²-2x-

2

y=0，经过椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的右焦点F及上顶点B，过圆外一点（m，0）（m＞a）倾斜角为

5π

6

的直线l交椭圆于C，D两点，
（1）求椭圆的方程；
（2）若右焦点F在以线段CD为直径的圆E的内部，求m的取值范围．

Answer 1

分析：（1）依据题意可求得F，B的坐标，求得c和b，进而求得a，则椭圆的方程可得；
（2）设出直线l的方程，与椭圆方程联立消去，利用判别式大于0求得m的范围，设出C，D的坐标，利用韦达定理表示出x₁+x₂和x₁x₂，进而利用直线方程求得y₁y₂，表示出

FC

和

FD

，进而求得

FC

•

FD

的表达式，利用F在圆E的内部判断出

FC

•

FD

＜0求得m的范围，最后综合可求得md 范围．

解答：解：（1）x2+y2-2x-

2

y=0过点F、B，
∴F（2，0），B(0，

2

)，
故椭圆的方程为

x2

6

+

y2

2

=1
（2）直线l：y=-

3

3

(x-m)(m＞

6

)

x2 6 + y2 2 =1 y=- 3 3 (x-m)

消y得2x²-2mx+（m²-6）=0
由△＞0?-2

3

＜m＜2

3

，
又m＞

6

?

6

＜m＜2

3

设C（x₁，y₁）、D（x₂，y₂），则x₁+x₂=m，x1x2=

m2-6

2

，y1y2=

1

3

x1x2-

m

3

(x1+x2)+

m2

3

，

FC

=(x1-2，y1)，

FD

=(x2-2，y2)
∴

FC

•

FD

=(x1-2)(x2-2)+y1y2=

2m(m-3)

3

∵F在圆E的内部，∴

FC

•

FD

＜0?0＜m＜3，
又

6

＜m＜2

3

?

6

＜m＜3．

点评：本题主要考查了直线与圆锥曲线的综合问题．考查了学生综合运用所学知识解决实际问题的能力．